Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 71

Considere um mancal de 30   c m   de comprimenro lubrificado com óleo cuja viscosidade é de 0,1   k g / m   × s a 20 ℃ no início da operação e 0,008   k g / m   × s     na temperatura operacional constante prevista de 80 ℃ . O diâmetro do eixo é de 8   c m   e a folga média entre o eixo e o casquilho é de 0,08   c m . Determine o torque necessário para vencer o atrito inicialmente e durante a operação quando o eixo gira a 500   r p m .

Passo 1

Pra a gente entender melhor, bora fazer um esqueminha!!

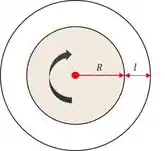
Aqui a gente tem um esquema de um mancal, são dois cilindros concêntricos de comprimento L = 30   c m . O diâmetro do eixo, ou diâmetro do cilindro maior, D = 8   c m e o espaço entre os dois cilindros é a folga média dita no enunciado l = 0,08   c m .

Para resolver essa questão, vamos recorrer a seguinte expressão:

T = μ 4 π R 3 n ˙ L l

Onde, μ ,   R ,   n ˙ ,   L   e   l são, respectivamente: Viscosidade do fluido, raio do eixo, número de rotações por segundo, comprimento e a folga entre os dois cilindros.

Já deu pra reconhecer algumas das variáveis que a gente tem, certo? Então agora precisamos deixar todo mundo nas unidades certas e bonitinhos para substituirmos na fórmula!

A viscosidade ta ok!

A gente tem o diâmetro em centímetro, precisamos transformar em raio e passar para metro:

R = D 2 = 8   c m 2 × 1   m 10 2   c m = 4 × 10 - 2   m

Temos o número de rotações em r p m , ou seja, rotações por minuto. Precisamos parassar para rotações por segundo:

diâmetro do eixo de 8 c m e a folga entre

n ˙ = 500   r o t a ç õ e s m i n × 1 m i n 60   s e g u n d o s = 8,33 r o t a ç õ e s s e g u n d o

L esta em c m , precisamos passar para m .

L = 30   c m × 1   m 10 2   c m = 0,3   m  

A folga entre os dois cilindros também precisa ser convertida para m .

l = 8 × 10 - 2   c m × 1   m 10 2   c m = 8 × 10 - 4   m  

Agora podemos resolver!

Passo 2

Substituindo as informações na fórmula:

T = μ 4 π 2 R 3 n ˙ L l

Para a operação na temperatura T = 20 ℃ e μ = 0,1   k g / m   × s :

T = 0,1 × 4 π 2 ( 4 × 10 - 2 ) 3 × 8,33 × 0,3 8 × 10 - 4  

Calculando:

T = 0,79   N × m

Agora para operação em T = 80 ℃ e μ = 0,008   k g / m   × s :

T = 0,008   × 4 π 2 ( 4 × 10 - 2 ) 3 × 8,33 × 0,3 8 × 10 - 4  

Calculando:

T = 0,063   N × m

Prontinho!!!

Resposta

Para a operação na temperatura 20 ℃ : T = 0,79   N × m  

Agora para operação em 80 ℃   : T = 0,063   N × m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O viscosímetro do Problema 2.67 foi usado para medir a viscosidade aparente de um fluido. Os dados abaixo foram obtidos. Que tipo de fluido não newtoniano é este? Determine os valores para k e n usado
Uma seção reta de um mancal giratório é mostrada. O membro esférico gira com velocidade angular ω, a uma pequena distância, a, acima da superfície plana. A folga estreita é preenchida com óleo viscoso
Uma bola de golfe americana é exibida no Problema 1.42. Para definir uma massa de bola e sua incerteza como dados, determine uma precisão com que o diâmetro da bola deve ser medido para sua massa espe
Uma bomba de tipo seringa é usada para bombear líquido a uma vazão de 100m L/m i n . O projeto para o pistão é tão incerteza na velocidade do pistão é de 0,00125c m , e o diâmetro interno do cilindro
A altura de um edifício pode ser estimada em uma distância horizontal horizontal até um ponto no solo e o ângulo desse ponto ao topo do edifício. Supondo que essas medições sejam L=30±0,15m e θ=30±0,2