Uma aleta anular com espessura t é usada como um radiador para dissipar calor de um sistema de potência espacial. A aleta tem sua parte inferior termicamente isolada e pode estar exposta à irradiação solar GS. A aleta está revestida com um material difuso espectralmente seletivo, cuja refletividade espectral é especificada.

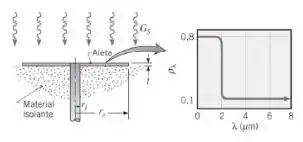
O calor é conduzido para a aleta através de um bastão sólido de raio ri e a superfície superior da aleta (superfície exposta) irradia para o espaço livre, que pode ser considerado a uma temperatura igual ao zero absoluto.

1. Se a condução através do bastão mantém uma temperatura na base da aleta de T(ri) = Tb = 400 K e a eficiência da aleta é de 100%, qual é a taxa de dissipação de calor em uma aleta com raio re = 0,5 m? Considere dois casos. No primeiro, o radiador está exposto ao Sol com GS = 1000 W/m2 ; e no segundo não há exposição do radiador (GS = 0).
2. Na prática, a eficiência da aleta será inferior a 100% e sua temperatura irá diminuir com o aumento do raio. Partindo de um volume de controle apropriado, deduza a equação diferencial que determine a distribuição radial de temperaturas na aleta em condições de regime estacionário. Especifique as condições de contorno apropriadas.

Começando pela letra a, precisamos encontrar a taxa de dissipação de calor, nos dois casos dados… Vamos lá!

Podemos usar a seguinte equação para calcular ela:

Lembrando que:

Vamos ter:

Show! Agora só falta a gente encontrar o valor de , para o primeiro caso, vamos fazer o seguinte:

Para encontrar o , vamos fazer assim:

Visitando a tabela 12.2, vamos ter que:

Agora sim! Voltando na equação, teremos:

Agora para o segundo caso nosso , será diferente, pois a , ficando assim:

Indo lá na tabela 12.2:

Teremos então:

Agora vamos calcular as duas taxa de dissipação, vamos ter:

Na segunda situação vamos ter que a taxa de dissipação será:

Prontinhos! Agora partiu letra b!

Agora na letra b, vamos encontrar a distribuição radial de temperaturas na aleta… Para isso vamos fazer um balanço de energia:

E sendo:

Vamos ficar com o seguinte:

Conseguimos! Arrasamos!!