Uma toalha molhada está pendurada em uma corda de roupas sob condições nas quais uma superfície recebe irradiação solar de GS = 900 W/m2 e as duas superfícies estão expostas à radiação da atmosfera (céu) e do solo de Gatm = 200 W/m2 e Gsolo = 250 W/m2 , respectivamente. Sob condições de vento moderado, o escoamento do ar, a uma temperatura de 27°C e a uma umidade relativa de 60%, mantém um coeficiente de transferência de calor por convecção de 20 W/(m2 · K) em ambas as superfícies da toalha. A toalha molhada tem uma emissividade de 0,96 e uma absortividade solar de 0,65. Como uma primeira aproximação, as propriedades do ar atmosférico podem ser calculadas a uma temperatura de 300 K.

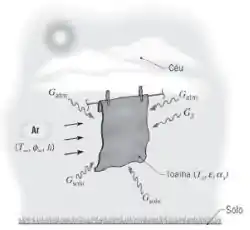
Determine a temperatura Ts da toalha. Qual é a taxa de evaporação correspondente para uma toalha que tem 0,75 m de largura e 1,5 m de comprimento?

Agora partiu continhas, ok?

Primeiro vamos começar usando o nosso balanço de energia:

Sendo esse , o seguinte:

Precisamos encontrar o , usando a equação 6.60, com , vamos ter:

Show! Vamos ficar com:

Agora substituindo na nossa equação principal e colocando nela todos os valores que temos, ficamos com:

Nessa parte aqui vamos precisar fazer uma coisa chatinha… Mas não é difícil, relaxa!

Precisaremos chutar valores para , com esse valor vamos na tabela A-6, do apêndice e encontraremos e , depois colocamos na equação e vemos se um lado dá o mesmo resultado do outro lado, ok?

Quando isso acontecer, vamos saber o nosso valor da temperatura superficial… Assumindo que nossa temperatura será , vamos ter:

Testando na nossa equação teremos:

Opa! Como o valor deu bem próximo podemos considerar que encontramos nossa temperatura sim!!

Agora para encontrar a taxa de evaporação faremos:

Uhull! Conseguimos!