Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 108
A aplicação de tintas de alta emissividade em superfícies radiantes é uma técnica normalmente usada para aumentar a transferência de calor por radiação.
- Para grandes placas paralelas, determine o fluxo térmico radiante através do espaço entre elas quando as superfícies estão a T1 = 350 K, T2 = 300 K, ε1 = ε2 = εs = 0,85.
- Determine o fluxo térmico radiante quando uma camada muito fina de uma tinta de alta emissividade, εt = 0,98, é aplicada nas duas superfícies.
- Determine o fluxo térmico radiante quando as camadas de tinta têm, cada uma, uma espessura L = 2 mm e a condutividade térmica da tinta é .
- Represente graficamente o fluxo térmico através do espaço para as superfícies sem revestimento como uma função de εs, com 0,05 ≤ εs ≤ 0,95. Mostre no mesmo gráfico os fluxos térmicos para as superfícies pintadas com a camada muito fina e com a camada de espessura L = 2 mm.
Passo 1
Animados para seguir que eu sei, não é?
Vamos desenhar as situações acima:
Beleza, a letra (a) nos pede o fluxo radiante quando temos as placas paralelas, ou seja, não temos a tinta!
Se lembram da fórmula para o fluxo radiante?
Lembrando que:
Então:
A letra (a) foi moleza, não foi?
A letra (b) é igual, mas agora nós temos uma fina camada de tinta, e assim a emissividade vai mudar, como vimos no desenho:
Passo 2
Shoow de bola !! Agora vamos para a letra (c) !!
Nela nós queremos determinar o fluxo térmico radiante quando as camadas de tinta têm, cada uma, uma espessura L = 2 mm e a condutividade térmica da tinta é .
Neste caso nós teremos a resistência condutiva ocorrendo na tinta e o fluxo radiante entre as duas camadas de tinta, ok?
Vamos ver o fluxo de calor ?
Se já sabemos que:
Então:
Como o calor que passa através das resistências é o mesmo:
Usando um software nós obtemos:
E chegamos na nossa resposta !!
Passo 3
Para finalizar, a letra (d) nos pede para achar o fluxo térmico através do espaço para as superfícies sem revestimento como uma função de com . E também mostrar no mesmo gráfico os fluxos térmicos para as superfícies pintadas com a camada muito fina e com a camada de espessura L = 2 mm.
Repetindo os que fizemos anteriormente:
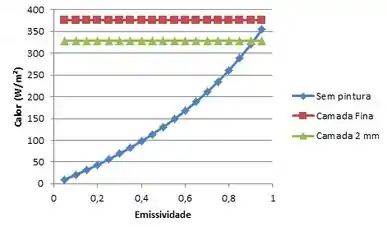
E é isso aí galerinhaaa !!
