Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 51

13.51 Considere o sistema de descarte de calor em espaçonaves do Problema 13.27, mas sob condições nas quais as superfícies 1 e 2 não podem ser aproximadas por corpos negros.

  1. Para superfícies isotérmicas com temperatura T = 325 K e emissividade ε = 0,7, e uma seção em U com largura W = 25 mm e comprimento L = 125 mm, determine a taxa, por unidade de comprimento (normal à página), na qual radiação é transferida de uma seção para o espaço.

  2. Explore o efeito da emissividade na taxa de descarte de calor e compare os seus resultados com aqueles para emissão exclusivamente a partir da base da seção.

Passo 1

Vamos lá!!

Antes de tudo, vamos relembrar o problema 13 - 23 , tinhamos uma espacionave com aletas retangulares e essas aletas eram cobertas com um material negro, a diferença é que agora não vamos considerar mais as superfícies um corpo negro!

Vamos desenhar um esqueminha do problema 13 - 23 , mas com os dados do nosso problema:

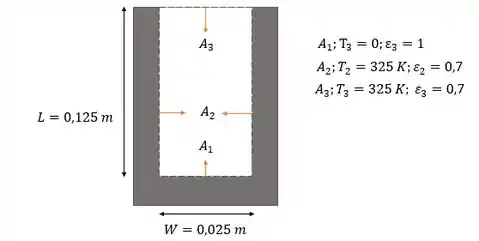
Lembrando que ε 2 = 1 porque se trata de uma abertura!!

Para a letra a, a gente quer a taxa de radiação por unidade de comprimento que esta sendo transferida para o espaço:

q 12 ' = q 12 l

Se A é a área de qualquer uma das superfícies, podemos fazer:

A ' = A l

Sendo l o comprimento! Por se tratar de uma cavidade com duas superfícies, então podemos usar a equação 13.23 do livro:

q 12,3 = σ T 1 2 4 - T 3 4 1 - ε 12 ε 12 A 12 + 1 A 12 F 12,3 + 1 - ε 3 ε 3 A 3

Dividindo pelo comprimento:

q ' 12 , 3 = σ T 1 2 4 - T 3 4 1 - ε 1 2 ε 1 2 A ' 1 2 + 1 A ' 1 2 F 12 , 3 + 1 - ε 3 ε 3 A ' 3

Como ε 3 = 1 e T 3 = 0 :

q ' 12,3 = σ T 12 4 1 - ε 12 ε 12 A ' 12 + 1 A ' 12 F 12,3

Passo 2

Vamos ver então o que a gente precisa pra poder substituir os valores e achar q 12,3 !!

Aqui A 12 ' é a soma de A 1 ' com A 2 ' ,

A 12 ' = W + 2 L

Agora falta F 12,3 , pela regra da reciprocidade:

F 3,12 A ' 3 = F 12,3 A 12 '

E:

A ' 3 = W

F 3,12 = 1 , já que estamos falando de uma abertura!!

Ficamos com:

q ' 12,3 = σ T 12 4 1 - ε 12 ε 12 ( W + 2 L ) + 1 F 3,12 W

Sabendo que σ = 5,67 × 10 - 8 W / m 2 K 4 , podemos substituir e calcular:

q ' 12,3 = 5,67 × 10 - 8 325 4 1 - 0,7 0,7 ( 0,025 + 2 × 0,125 ) + 1 0,025

Achamos:

q 12,3 ' = 15,2   W / m

Passo 3

  1. Explore o efeito da emissividade na taxa de descarte de calor e compare os seus resultados com aqueles para emissão exclusivamente a partir da base da seção.

Agora para letra b temos que fazer duas coisas!! Queremos ver o efeito da emissividade em q 12,3 ' e q 1 ' ! Mas quem é q 1 ' ??

Estamos considerando a taxa ocorra apenas a partir da base A 1 , nesse caso teriamos:

q ' 1 = A 1 ' σ ε 1 T 1 4

Para ε = 0,7 :

q ' 1 = 0,025 × 5,67 × 10 - 8 × 0,7 × 325 4 = 11,1   W / m

Mas a gente quer conhecer o efeito da emissividade de uma forma geral, então vamos montar um gráfico com duas curvas, usando :

q ' 12,3 = σ T 12 4 1 - ε ε ( W + 2 L ) + 1 F 3,12 W

E:

q ' 1 = A 1 ' σ ε T 1 4

E variando ε entre 0,1 e 1 :

O que a gente consegue observar é que o aumento da emissividade causa um aumento na taxa de radiação!!

Resposta

q 12,3 ' = 15,2   W / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um orifício com fundo plano e 6 mm de diâmetro é perfurado até uma profundidade de 24 mm em um material cinza e difuso, que tem uma emissividade de 0,8 e uma temperatura uniforme de 1000 K. Determine
Considere duas placas paralelas muito grandes com superfícies cinzas e difusas. Determine a irradiação e a radiosidade na placa superior. Qual é a radiosidade da placa inferior? Qual é a troca de radi
Considere uma janela de vidro duplo. A superfície do vidro pode ser tratada com um revestimento de baixa emissividade para reduzir sua emissividade de ε = 0,95 para ε = 0,05. Determine o fluxo térmico
Considere uma longa fenda em forma de V, com profundidade de 10 mm, usinada em um bloco mantido a 1000 K. Se as superfícies da fenda são difusas e cinzas com uma emissividade de 0,6, determine o fluxo
Nos Problemas 12.20 e 12.25, estimamos a temperatura da superfície da Terra supondo que a Terra fosse negra. A maioria da superfície da Terra é água, que tem uma emissividade hemisférica de ε = 0,96.