Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 115
Considere o tubo e a barreira de radiação do Problema 13.49, mas agora leve em consideração a convecção natural no espaço entre o tubo e a barreira.
- Qual é a taxa de transferência de calor total, por unidade de comprimento, entre o tubo e a barreira?
- Explore o efeito de variações no diâmetro da barreira na taxa de transferência de calor total, assim como nas contribuições da convecção e da radiação.
Passo 1
Animados para seguir que eu sei, não é?
Nós queremos achar aqui qual é a transferência de calor, ok?
Podem ocorrer perda de calor por duas formas, radiação e condução!!
A radiação para cilíndricos concêntricos vocês já sabem:
A área é dada por:
Então:
O problema nos disse que:
Substituindo:
Passo 2
O calor convectivo é dado por:
Sabendo que:
Vamos lembrar também que:
Para as propriedades do ar nós precisamos da temperatura média:
Olhando na Tabela A – 4 para achar as propriedades do ar a uma temperatura a :
Substituindo:
Substituímos:
E o total:
E chegamos ao fim da letra (a)!!
Passo 3
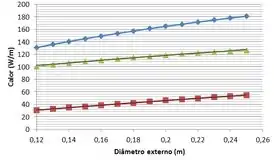
Para a letra (b) nós devemos avaliar o efeito de variações no diâmetro da barreira na taxa de transferência de calor total, assim como nas contribuições da convecção e da radiação, ou seja, faremos tudinho de novo !!
Usando um software para facilitar:
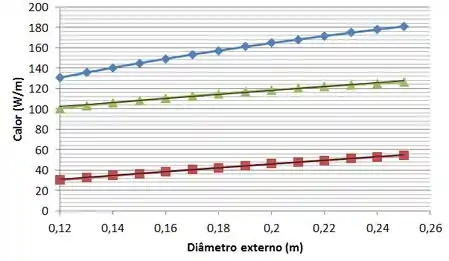
E é isso aí galerinhaaa !!
