Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 32
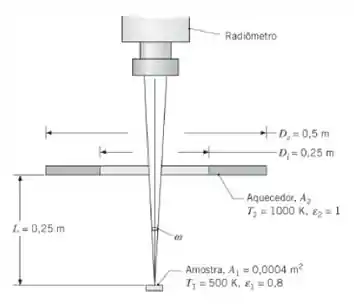
Um radiômetro avista um pequeno alvo (1) que está sendo aquecido por um aquecedor com a forma de um anel (2). O alvo tem uma área A1 = 0,0004 m², uma temperatura T1 = 500 K, e uma emissividade difusa e cinza ε1 = 0,8. O aquecedor opera a T2 = 1000 K e tem uma superfície negra. O radiômetro avista toda a área da amostra (alvo) com um ângulo sólido de
ω = 0,0008 sr.
- Escreva uma expressão para a potência radiante deixando o alvo que é coletado pelo radiômetro, em termos da radiosidade do alvo J1 e de parâmetros geométricos relevantes. Deixe-a na forma simbólica.
- Escreva uma expressão para a radiosidade do alvo J1 em termos da sua irradiação, poder emissivo e propriedades radiantes apropriadas. Deixe-a na forma simbólica.
- Escreva uma expressão para a irradiação sobre o alvo, G1, devido à emissão a partir do aquecedor, em termos do poder emissivo do aquecedor, da área do aquecedor e de um fator de forma apropriado. Use essa expressão para avaliar numericamente G1.
- Use as expressões e os resultados anteriores para determinar a potência radiante coletada pelo radiômetro.
Passo 1
Vamos que vamos galerinha ?!
Bom, na letra (a) nós queremos achar a expressão para a potência radiante deixando o alvo que é coletado pelo radiômetro, em termos da radiosidade do alvo J1 e de parâmetros geométricos relevantes, ok?
Bom, o capítulo 12 nos trouxe duas fórmulas que podemos usar neste caso! A primeira:
Mas ainda não apareceu a radiosidade, certo? Então para isso nós usaremos a segunda relação:
Substituindo:
Chegamos ao que queríamos !!
Passo 2
Na letra (b) nós queremos uma expressão para a radiosidade do alvo J1 em termos da sua irradiação, poder emissivo e das propriedades radiantes apropriadas !!
E aqui o capítulo 12 nos trás mais uma fórmula para usarmos:
Vamos ver como escrevemos cada uma delas?
Sendo assim:
Mais uma tranquilinha, certo?
Passo 3
A letra (c) nos pede outraa expressão, mas agora para a irradiação sobre o alvo, G1, devido à emissão a partir do aquecedor, em termos do poder emissivo do aquecedor, da área do aquecedor e de um fator de forma apropriado !!
Vamos lembrar que:
Onde é o calor radiante que deixa (2) e é interceptado por (1)! Este calor pode ser reescrito como:
Então:
Usando a reciprocidade:
Substituindo:
O fator de forma pode ser escrito como:
Usando a equação apropriada para este caso:
E lembrando que:
Então:
Sabendo que:
Então:
E assim nós finalizamos a (c) !!
Passo 4
Shoow de boola, agora vamos seguindo para a letra (d) !!
Nela nós queremos determinar a potência radiante coletada pelo radiômetro, ou seja, vamos usar a equação que achamos em (a) para conseguir uma resposta !!
Começando pela letra (b):
E substituindo
Sabemos que:
Então:
E lembrando lá da equação da letra (a):
Sabemos que:
Substituindo:
Sucessooo galerinhaa, terminamos mais umaa !!