Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 34
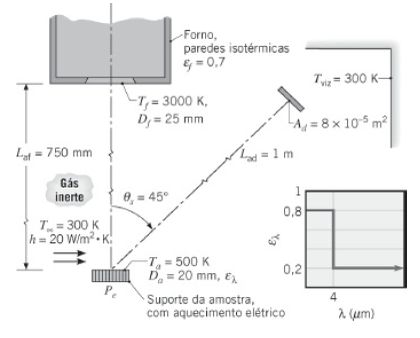
Uma amostra aquecida eletricamente é mantida com uma temperatura superficial Ta = 500 K. O revestimento da amostra é difuso, porém espectralmente seletivo, com a distribuição da emissividade espectral mostrada na figura. A amostra é irradiada por um forno localizado
coaxialmente a uma distância Laf = 750 mm. O forno tem paredes isotérmicas com uma emissividade εf = 0,7, que estão a uma temperatura uniforme Tf = 3000 K. Um detector de radiação com área Ad = 8 × 10–5 m² está posicionado a uma distância Lad = 1,0 m da amostra, ao longo de uma direção que está a 45° da normal à amostra. O detector é sensível à potência radiante espectral somente na região espectral compreendida entre 3 e 5 μm. Na superfície da amostra há transferência de calor por convecção com um gás com e . A vizinhança da amostra é grande e encontra-se a uma temperatura uniforme de .
- Determine a potência elétrica, , necessária para manter a amostra a Ta = 500 K.
- Considerando tanto a emissão como a irradiação refletida a partir da amostra, determine a potência radiante que incide sobre o detector na região espectral compreendida entre 3 e 5 μm.
Passo 1
Vamos que vamos galerinha ?!
Bom, na letra (a) nós queremos achar a potência elétrica, , necessária para manter a amostra a Ta = 500 K, não é?
Bom, a amostra recebe calor por meio da potência elétrica fornecida, , irradiação absorvida do forno, , e irradiação absorvida do ambiente, , enquanto perde calor por convecção, e emissão, .
Substituindo os calores no balanço:
O calor convectivo nós sabemos como calcular, basta lembrarmos que:
Então:
Para , nós precisamos obter algumas coisas !! Vamos lembrar que:
Em
Vamos ver o que ainda não sabemos:
O fator forma para discos coaxiais é dado por:
Onde:
Lembrando que:
Substituindo:
E o fator de forma:
Nós ainda precisamos achar , certo?
Para ela nós também temos uma fórmula:
Como , olhando na tabela 12.1:
Como mostrado na figura do problema:
Então:
Agora sim !! Mão a obra para achar o calor:
Passo 2
Bom, ainda precisamos de mais duas formas de transferência de calor!!
Começando por:
Vamos começar calculando
Para seguimos o mesmo raciocínio do Passo anterior:
Como , olhando na tabela 12.1:
Então:
Agora é só achar o calor:
E o último calor que precisamos calcular é o emissivo:
A emissividade é calculada igualzinho à absortividade:
Como , olhando na tabela 12.1:
Então:
Agora é só substituir:
E a potência:
Chegamos ao fim da letra (a) !!
Passo 3
Shoow de boola, agora vamos seguindo para a letra (b) !!
Para a letra (b) nós queremos achar determine a potência radiante que incide sobre o detector na região espectral compreendida entre 3 e 5 μm, considerando tanto a emissão como a irradiação refletida a partir da amostra !!
Neste caso nós vamos usar a equação:
Temos que:
Agora vamos calcular o que nós não temos !!
Olhando a Tabela 12.1:
Então:
Vamos seguindo:
Olhando a Tabela 12.1:
Então:
E para o próximo:
Olhando a Tabela 12.1:
Então:
E agora sim vamos calcular o que queremos:
Sucessooo galerinhaa, terminamos mais umaa !!