Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 3.Problemas - Ex. 27

Aproximadamente 10^6 componentes elétricos discretos podem ser colocados em um único circuito integrado, com uma dissipação térmica na ordem de 3000 w/m^2.

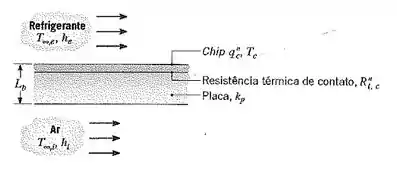
  1. Esboce o circuito térmico equivalente para condições de regime estacionário. Usando as variáveis, identifique a resistências apropriadas, as temperaturas e os fluxos térmicos.

Passo 1

Fala aí galerinha? Tudo bem com vocês? Bora pra cima! No item a), ele pede pra gente esboçar o circuito térmico equivalente. Dessa forma, temos:

No item b), calculando a temperatura do chip, vamos aplicar a conservação de energia para uma superfície de controle sobre o chip, ou seja:

E e n t r a - E s a i = 0

Logo,

q c - q i - q 0 = 0

Dessa forma:

q c = T c - T ∞ , i 1 h i + L k b + R t , c + T c - T ∞ , o 1 / h o

Passo 2

A parte boa, é que a questão nos deu que:

Substituindo os valores e encontrando T C que é a temperatura do chip:

q c = T c - T ∞ , i 1 h i + L k b + R t , c + T c - T ∞ , o 1 / h o

3 ⋅ 10 4 = T c - 20 ° C 1 40 + 0,005 1 b + 10 - 4 + T c - - 20 ° C 1 / 1000

Logo,

T C = 49 ° C

Por fim, calculando no item c) a máxima dissipação de calor para o dielétrico do liquido:

Para T c = 49 ° e h o = 1000

q c = 67,160   W / m 2

Consultando a tabela A - 2 , para o óxido de alumínio.

Resposta

a)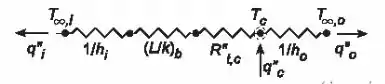

b) T C = 49 ° C

c) q c = 67,160   W / m 2

Exercícios de Livros Relacionados

Considere a água do Exemplo 1.5 como sendo inicialmente líquida em sua temperatura de fusão. A superfície da parede externa é repentinamente reduzida para T 1 = - 30 ° C , resultando na solidificação
Considere uma área de composta de altura total H = 20m m e espessura L = 30m m . A seção A tem espessura L A = 10m m , e as seções B e C cada uma tem altura H B = 10m m e espessura L B = 20m m . As te
24 – Duas paredes espessas são separadas por uma lacuna de vácuo de espessura L. Um cilindro de diâmetro D, passa entre as paredes. Todas as superfícies são altamente polidas (suas emissividades são m
10 - A sensação de calafrio (resfriamento pelo vento), que é experimentada em dias frios com vento, está relacionada ao aumento da transferência de calor na pele humana exposta à atmosfera circundante
Considere uma parede composta que inclui um painel lateral em madeira dura com 8 mm de espessura; travessas de suporte em madeira dura com dimensões de 40 mm por 130 mm, afastadas com 0,65 m de distân