Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 10
10 - A sensação de calafrio (resfriamento pelo vento), que é experimentada em dias frios com vento, está relacionada ao aumento da transferência de calor na pele humana exposta à atmosfera circundante. Considere uma camada de tecido gorduroso que possua de espessura e cuja superfície interna seja mantida a uma temperatura de . Em um dia calmo, o coeficiente de transferência de calor por convecção na superfície externa é de , mas com vento de ele chega a . Em ambos os casos, a temperatura do ar ambiente é de .
(a) Qual é a razão entre as perdas de calor, por unidade de área de pele, em um dia calmo e em um dia com vento?
(b) Qual será a temperatura da superfície externa da pele em um dia calmo? E em um dia com vento?
(c) Qual a temperatura que o ar deveria ter no dia calmo para causar a mesma perda de calor que ocorre com a temperatura do ar a em um dia com vento?
Passo 1
Para nos ajudar, vamos desenhar a rede térmica com suas respectivas resistências, como mostrado abaixo.
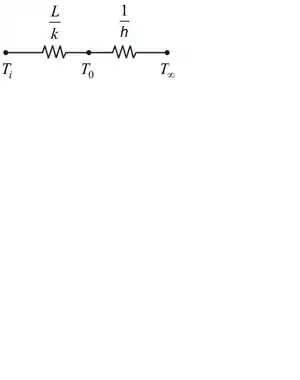
Passo 2
(a)
Obtenha as propriedades das propriedades termo físicas da tabela de outros materiais,
Condutividade térmica do tecido adiposo,.
De acordo com a lei de Fourier, o fluxo de calor em um dia calmo é dado pela equação, como mostrado abaixo.
Aqui, a condutividade térmica do tecido adiposo é , a espessura do tecido adiposo é , o coeficiente de transferência de calor por convecção em um dia calmo é e as temperaturas interna e ambiente são e .
Substituindo pelos valores fornecidos, temos:
Passo 3
De acordo com a lei de Fourier, o fluxo de calor em dia de vento é dado pela equação, como mostrado abaixo.
Aqui, a condutividade térmica do tecido adiposo é , a espessura do tecido adiposo é , o coeficiente de transferência de calor por convecção em um dia com vento é e as temperaturas interna e ambiente são e .
Passo 4
Calcule a taxa de perda de calor por unidade de área da pele para um dia calmo e para um dia ventoso.
Portanto, a razão entre as perdas de calor, por unidade de área de pele, em um dia calmo e em um dia com vento é .
Passo 5
b)
Como o fluxo de calor permanece constante em todo o sistema, o fluxo de calor na parte convectiva é o mesmo que o fluxo total.
Calcule a temperatura da superfície externa da pele em um dia calmo usando a equação mostrada abaixo.
Aqui, a temperatura da superfície externa da pele é .
Substitua os valores conhecidos na equação acima.
Portanto, a temperatura da superfície externa da pele em um dia calmo é .
Passo 6
Agora, vamos calcular a temperatura da superfície externa da pele em um dia ventoso usando a equação mostrada abaixo.
Substitua os valores conhecidos na equação acima.
Portanto, a temperatura da superfície externa da pele em um dia ventoso é .
Passo 7
c)
Calcule a temperatura do ar em dia calmo para produzir a mesma perda de calor, se a temperatura do ar em dia ventoso for .
Como, o fluxo de calor permanece constante em todo o sistema.
Portanto, o fluxo de calor do dia calmo é igual ao fluxo de calor do dia ventoso.
Substitua os valores conhecidos na equação acima.
Portanto, a temperatura em dia calmo deve ser .
Resposta
- 0,55
- e