Um aquecedor elétrico delgado é enrolado ao redor da superfície externa de um longo tubo cilíndrico cuja superfície interna é mantida a uma temperatura de 5°C. A parede do tubo possui raios interno e externo iguais a 25 e 75 mm, respectivamente, e uma condutividade térmica de 10 W/(m · K). A resistência térmica de contato entre o aquecedor e a superfície externa do tubo (por unidade de comprimento do tubo) é = 0,01 m · K/W. A superfície externa do aquecedor está exposta a um fluido com T∞ = –10°C, com um coeficiente convectivo h = 100 W/(m2 · K). Determine a potência do aquecedor, por unidade de comprimento do tubo, requerida para mantê-lo a Te = 25°C.
Passo 1
Beleza galerinha, vamos lá! Aplicação de um balanço de energia em uma superfície de controle sobre o aquecedor!
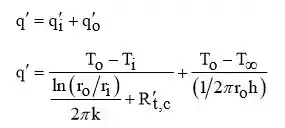
Passo 2
Selecionando valores nominais de k = 10 W/m⋅K, t,c R′ = 0,01 R′/W e h = 100 W/m⋅K, obtêm-se as seguintes variações paramétricas
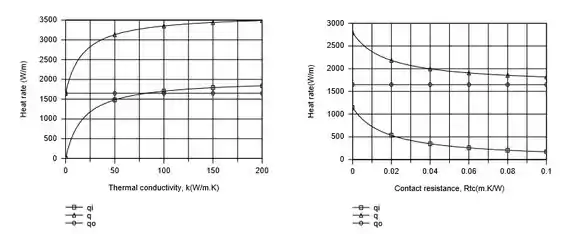
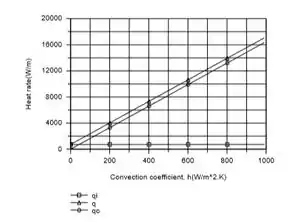
Para um valor prescrito de , é fixo, enquanto , e portanto aumenta e diminui, respectivamente, com aumento de e . Estas tendências são atribuíveis aos efeitos de e sobre a resistência total (condução mais contato) que separa o aquecedor da superfície interna. Para e fixo, é fixo, enquanto , e portanto aumenta com o aumento devido a uma redução na resistência de convecção.
Passo 3
E pra achar a potência do aquecedor, por unidade de comprimento é só ir substituindo tudo na equação: