Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 93

Reconsidere o Problema 3-92. Usando o software EES (ou outro), trace a taxa de transferência de calor da bola em função da espessura do isolamento plástico na faixa de 0,5 a 20 mm. Discuta os resultados.

Passo 1

Bora começar mais umaa??

Claroo que sim !!

Então galerinha, precisamos da taxa de transferência de calor, certo?

Para isso nós temos uma fórmula:

Q ˙ = T b o l a - T e x t R T o t a l

0

Sabemos que:

T b o l a = 50 ° C

T e x t = 15 ° C

Ainda não sabemos nada sobre a resistência total, só sabemos que teremos uma resistência à passagem de calor oferecida pelo isolamento e pela convecção externa:

R T o t a l = R i s o l + R c o n v

A resistência convectiva é dada por:

R c o n v = 1 h e x t A e x t

E como o isolamento é esférico:

R i s o l = r e x t - r i n t 4 π k i s o l r e x t r i n t

Beleza! Já temos tudo o que precisamos? Que nada !! Falta a área e o raio externo.

Como calculamos??

Para esferas a área é dada por:

A e x t = π D e x t 2

Lembrando que o diâmetro externo é o diâmetro interna mais duas vezes o comprimento da espessura:

A e x t = π D i n t + 2 L i s o l 2

Seguindo a mesma analogia:

r e x t = r i n t + L i s o l

Substituímos tudo nas fórmulas da resistência:

R c o n v = 1 h e x t π D i n t + 2 L i s o l 2

R i s o l = ( r i n t + L i s o l ) - r i n t 4 π k i s o l ( r i n t + L i s o l ) r i n t = L i s o l 4 π k i s o l ( r i n t + L i s o l ) r i n t

Passo 2

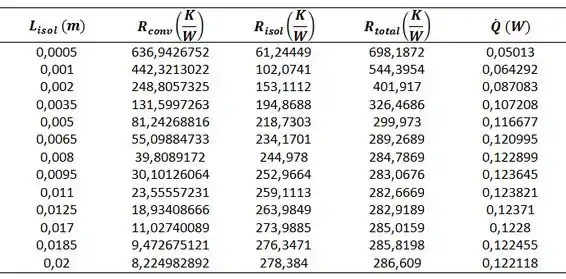
Usando o programa Excel e lembrando que:

h e x t = 20 W m 2 . K

k i s o l = 0,13 W m . K

D i n t = 0,004   m

r i n t = 0,002   m

E agora nós variamos a espessura do isolamento e, consequentemente, nossa taxa de transferência de calor:

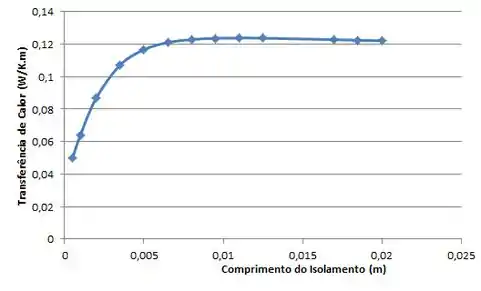
Traçando o gráfico:

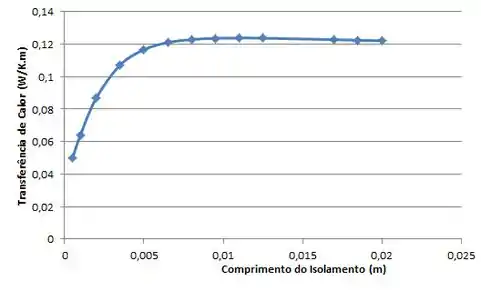
Ou seja, a transferência de calor aumenta até certo ponto. A partir daí a transferência de calor decai levemente.

O que isso indica? Que atingimos o raio crítico !!

Gostaram dessa ?!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A taxa de transferência de calor da parede de um tubo circular com convecção agindo sobre a superfície externa é dada, por unidade de seu comprimento, q ˙ = 2 π L T i - T o ln ⁡ r o / r i k + 1 r o h
Um tanque de armazenamento de oxigênio líquido de hospital de 1m de diâmetro mantém o oxigênio líquido a 90K . O reservatório é constituído por uma casca de alumínio k = 170W / m ⋅ K de 0,5c m de espe
Um tanque de armazenamento de oxigênio líquido de hospital de 1m de diâmetro interno mantém o oxigênio líquido a 90K . O reservatório é constituído por uma casca de alumínio k = 170W / m ⋅ K de 0,5c m
Vapor a 200 °C flui em um tubo de ferro fundido ( k = 80W / m ⋅ K ) cujos diâmetros interno e externo são D 1 = 0,20m e D 2 = 0,22m , respectivamente. O tubo é coberto com isolante de lã de vidro ( k
Um tubo é isolado de forma que o raio externo do isolamento seja menor que o raio crítico. Agora o isolamento é retirado. A taxa de transferência de calor do tubo aumentará ou diminuirá para a mesma t