A superfície interna de uma parede plana é isolada e a superfície externa está exposta a uma corrente de ar a . A parede se encontra a uma temperatura uniforme correspondente à da corrente de ar. De repente, uma fonte de calor radiante é ligada, ocasionando a incidência de um fluxo térmico uniforme sobre a superfície externa.

(a) Esboce e identifique, em coordenadas , as distribuições de temperaturas: inicial, em regime estacionário e em dois tempos intermediários.
(b) Esboce o fluxo térmico na superfície externa como uma função do tempo.
Passo 1
Queremos nessa questão (a) esboçar a distribuição da temperatura em coordenadas, , e (b) esboçar o fluxo de calor na superfície externa, em função do tempo.
Nos foi dito no problema que a superfície interior da parede plana é isolado enquanto que a superfície externa é exposta a uma corrente de ar com temperatura . A parede está a uma temperatura uniforme correspondente à da corrente de ar. Uma fonte de calor de radiação é ativada através da aplicação de um fluxo uniforme na superfície externa.
PRESSUPOSTOS:
(1) Condução unidimensional;
(2) Propriedades constantes;
(3) Nenhuma geração interna, ;
(4) Superfície em é perfeitamente isolada;
(5) Toda a energia radiante incidente é absorvida e troca insignificante de radiação com o ambiente.
Passo 2
(a) Queremos plotar às distribuições de temperatura para quatro condições de tempo, incluindo a distribuição inicial, , e a distribuição em estado estacionário, .
Temos que a distribuição de temperatura em uma parede plana é uma função da espessura da parede e do tempo . Para a condição inicial, o gradiente em é sempre zero e a temperatura é igual à temperatura da corrente de ar e o gráfico varia linearmente. Nos tempos intermediários, o gradiente é mais acentuado e a temperatura em relação a varia. Para o estado estacionário, a distribuição de temperatura na parede plana é reta, pois a temperatura é constante em relação ao tempo, assim, o fluxo radiante é igual ao fluxo de calor convectivo.
Assim, temos as seguintes condições iniciais e de contorno:
Como a temperatura inicial da parede é uniforme, então
Como a superfície interna da parede plana é isolada em , então
Pelo balanço de energia da superfície em , temos que
Passo 3
Agora, pelo que foi dito acima, podemos desenhar as distribuições de temperatura coordenadas da seguinte maneira:
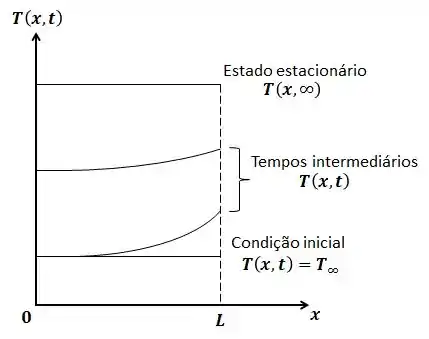
Passo 4
(b) A expressão do fluxo de calor na superfície externa pode ser dada pela seguinte expressão:
Assim, o gráfico varia exponencialmente. Podemos desenhar o fluxo de calor na superfície externa em função do tempo da seguinte maneira:
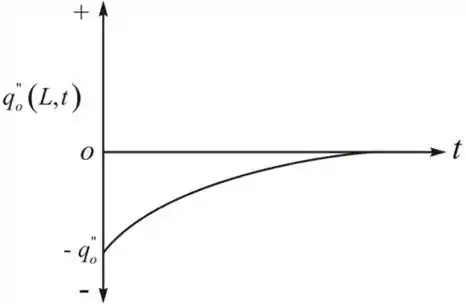
Resposta
Ei, a resposta está no passo a passo :)