Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 37

Considere o tubo e as condições de entrada do Problema   1.36 . Uma taxa de transferência de calor de q   =   3,89   M W   é transferida para o tubo. Para uma pressão na saída de p   =   8   b a r , determine (a) a temperatura da água na saída do tubo, assim como a variação na (b) a energia térmica combinada com o trabalho de fluxo; (c) energia mecânica; (d) energia total da água entre a entrada e a saída do tubo. Sugestão: Como uma primeira estimativa, despreza a variação na energia mecânica ao resolver a parte (a). Propriedades relevantes podem ser obtidas em textos de termodinâmica.

Passo 1

Essa questão é tipo a irmã da questão anterior, beleza? Então nós vamos usar como base a mesma ilustração de antes mudando apenas que agora nós temos o valor de q e não temos a temperatura de saída do tubo.

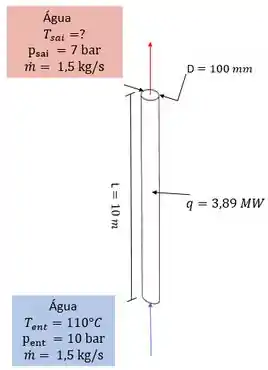
O enunciado nos pede para calcular a temperatura da água de saída do tubo, a energia térmica combinada com o trabalho de fluxo, a energia mecânica e a energia total. Então vamos lá!

Passo 2

Repara que aqui vamos começar com o que era a última alternativa na questão anterior. Então para a letra (a) vamos utilizar:

q = Ė g = m ˙ c p ( T s a i - T e n t )

Substituindo os valores (lembrando de colocar a temperatura em K ),

3,89 × 10 6 W = 1,5 k g s × 4,222 × 10 3 k J k g . K ( T s a i - 383 K )

Assim, encontramos uma temperatura de saída do tubo de:

T s a i = 997,2   K = 724,2   ° C

Passo 3

A resposta da letra (b) vai ser a mesma que a questão anterior, ou seja:

Ė e n t = 118,5   K W

Ė s a i = 83,0   k W

E a letra (c), pede que calculemos a energia mecânica, o que já vimos ser:

q = Ė g = 3,89   M W

Passo 4

Por último, a energia total da água vai ser calculada através da equação:

Ė a c u = Ė e n t + Ė g -   Ė s a i  

Substituindo os valores,

Ė a c u = 118,5   K W + 3890   k W - 83,0   k W

Ė a c u = 3,93   M W

Resposta

  1. T s a i = 724,2   ° C
  2. Ė e n t = 118,5   K W e Ė s a i = 83,0   k W  
  3. Ė g = 3 , 89   M W
  4. Ė a c u = 3,93   M W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um reservatório esférico de aço inoxidável de 3 m de diâmetro interno e 1 cm de espessura é usado para armazenar uma mistura de água e gelo a 0°C. O tanque está localizado ao ar livre a 25°C. Assumind
Uma casa possui um sistema de aquecimento elétrico que consiste em um ventilador de 300 W e uma resistência elétrica de aquecimento, instalado em um duto. O ar escoa permanentemente através do duto a
O telhado de uma casa tem laje de concreto k = 2 W m K de 22 cm de espessura, 15 m de largura e 20 m de comprimento. A emissividade da superfície externa do telhado é de 0,9 e o coeficiente de transfe
O ar entra no duto de um sistema de ar condicionado a 100 kPa e 10°C com vazão volumétrica 15 m 3 m i n . O diâmetro do duto é de 24 cm, e o calor é transferido para o ar no duto a partir do meio exte
Os dutos de um sistema de aquecimento do ar passam por uma área não aquecida. Como resultado das perdas de calor, a temperatura do ar no duto cai em 3°C. Considerando que a vazão mássica do ar é de 90