Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 127
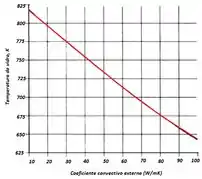
Um aquecedor a gás natural utiliza a combustão em um leito poroso de material catalítico para manter uma placa cerâmica, com emissividade εc = 0,95, a uma temperatura uniforme de Tc = 1000 K. A placa cerâmica encontra-se separada de uma placa de vidro por um espaço que contém ar, cuja espessura é L = 50 mm. A superfície do vidro é difusa e suas transmissividade e absortividade espectrais podem ser aproximadas por e para, e para , e e para . A superfície externa do vidro está exposta ao ar ambiente quiescente e a uma grande vizinhança, sendo . A altura e a largura do aquecedor são .
- Qual é a transmissividade total do vidro em relação à irradiação originada na placa cerâmica? O vidro pode ser aproximado como opaco e cinza?
- Nas condições especificadas, calcule a temperatura do vidro, , e a taxa de transferência de calor a partir do aquecedor,
- Um ventilador pode ser usado para controlar o coeficiente convectivo na superfície externa do vidro. Calcule e represente graficamente e como funções de para .
Passo 1
Animados para seguir que eu sei, não é?
Na letra (a) nós queremos achar transmissividade total do vidro em relação à irradiação originada na placa cerâmica, ok?
E para isso nós temos uma fórmula que podemos trazer lá do capítulo 12:
Sabendo que:
e para
e para
e para
Então:
Para acha-lo nós precisamos lembrar que:
E olhando a Tabela 12.1:
Então:
Bom, como a transmissão de radiação da cerâmica é tão pequena podemos presumir que a placa de vidro seja opaca a uma boa aproximação, então nós podemos aproximar o vidro pode como uma superfície cinza !
Passo 2
Na letra (b) nós queremos achar a temperatura do vidro, , e a taxa de transferência de calor a partir do aquecedor, , ok?
Como o calor está sendo transmitido no interior e no exterior na forma de convecção e fluxo radiante:
Substituindo:
Vamos ver o que temos?
Só precisamos achar os coeficientes convectivos, e para isso nós vamos usar as fórmulas:
Lembrando que:
Bom galera, como vocês viram todo depende da temperatura do vidro que queremos achar, então não tem jeito !! Nós precisamos dos softwares salvadores da pátria !!
Usando o IHT:
E com a temperatura nós podemos achar os calores:
Então o calor a partir do aquecedor:
Passo 3
Para finalizar, a letra (c) nos pede para representar graficamente a variação de e como funções de para .
Vamos ter que usar os softwares novamente para descobrir:
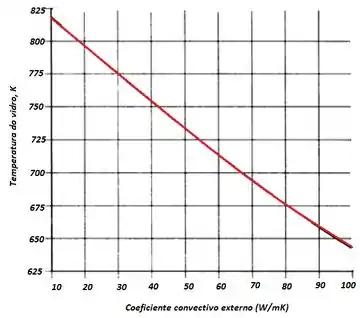
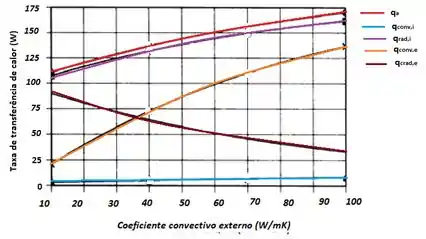
E é isso aí galerinhaaa !!
