Um coletor solar plano, constituído por uma placa absorvedora e uma única placa de cobertura, está inclinado com um ângulo τ = 60° em relação à horizontal.

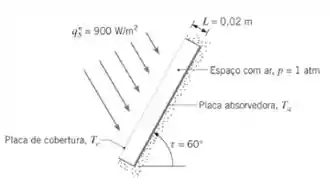
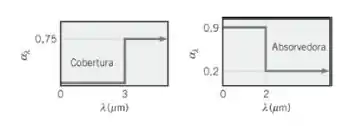
Considere condições nas quais a radiação solar incidente é colimada formando um ângulo de 60° em relação à horizontal e o fluxo solar é de . A placa de cobertura é perfeitamente transparente à radiação solar e opaca à radiação com comprimentos de onda mais longos. As placas de cobertura e de absorção são superfícies difusas, que apresentam as absortividades espectrais mostradas a seguir.

O comprimento e a largura das placas absorvedora e de cobertura são muito maiores do que o espaçamento entre elas, L. Qual é a taxa na qual a radiação solar é absorvida por unidade de área da placa absorvedora? Com a placa de absorção isolada termicamente na sua superfície inferior e temperaturas das placas de absorção e de cobertura, Ta e Tc, de 70°C e 27°C, respectivamente, qual é a perda térmica por unidade de área da placa absorvedora?

Na letra (b) nós queremos achar a perda térmica por unidade de área da placa absorvedora, sabendo que:

Se nós temos calor saindo por convecção e pelo fluxo radiante:

Para o calor convectivo:

O coeficiente convectivo pode ser calculado como:

Sabendo que:

Na fórmula:

Nós já sabemos que:

Para achar as propriedades do ar nós precisamos da temperatura média:

Assumindo que a temperatura seja próxima a e olhando na Tabela A – 4:

Substituindo:

Colocando no calor:

Para o fluxo radiante:

Como a radiação está concentrada nos maiores comprimento de onda:

Substituindo:

Somando:

Então o coletor perde calor a uma taxa de

E finalizamos mais umaa !!