Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 100

Ar na condição padrão escoa através de uma expansão súbita em um duto circular. Os diâmetros do duto a montante e a jusante da expansão são 75 mm e 225 mm, respectivamente. A pressão a jusante é 5 mm de água maior que aquela a montante. Determine a velocidade média e a vazão volumétrica do ar aproximando-se da expansão.

Passo 1

Neste problema é pedido a velocidade média e a vazão volumétrica defluido em uma tubulação que sofe expansão, conforme Figura abaixo:

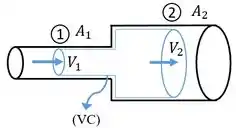
Será utilizada a Equação da energia na forma:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l m

Sendo a perda de carga menor (de expansão) definida como:

h l m = K V 1 2 2

Como hipótese e dados do enunciado tem-se que;

- regime permanente ( ∂ / ∂ t = 0 );

- escoamento horizontal ( z 1 = z 2 );

- escoamento incompressível ( ρ 1 = ρ 2   e ρ a r = 1,23   k g / m 3 );

- α ≈ 1,0 ;

- D 1 = 75   m m ;

- D 2 = 225   m m ;

- p 2 - p 1 = ρ á g u a g ∆ h (foi dado aumento de pressão em termos de altura de água, por isso o uso a expressão de pressão estática);

- ∆ h = 5   m m .

Passo 2

Usando a Equação de Energia, em J/kg, entre as seções 1 e 2:

p 1 ρ 1 + α V 1 2 2 + g z 1 = p 2 ρ 2 + α V 2 2 2 + g z 2 + h l m

p 2 ρ - p 1 ρ = α V 1 2 2 - α V 2 2 2 + g z 1 - g z 2 - h l m

p 2 - p 1 = ρ α V 1 2 - V 2 2 2 + ρ g z 1 - z 2 - ρ h l m

Sabendo a expressão de h l m , que z 1 = z 2 e α ≈ 1 :

p 2 - p 1 = ρ V 1 2 - V 2 2 2 - ρ K V 1 2 2

Passo 3

Como é buscada a vazão volumétrica é necessário obter a velocidade do escoamento, então escrevendo a velocidade V 2 em função de V 1 a partir da equação da continuidade:

Q 1 = Q 2

V 1 π D 1 2 4 = V 2 π D 2 2 4

V 2 = V 1 D 1 2 D 2 2

Passo 4

Reescrevendo a expressão dobtida no Passo 2:

p 2 - p 1 = V 1 2 - V 2 2 2 - ρ K V 1 2 2

p 2 - p 1 = V 1 2 - V 1 D 1 2 D 2 2 2 - ρ K V 1 2 2

p 1 - p 2 = ρ V 1 2 2 1 - D 1 2 D 2 2 2 - K

Passo 5

Isolando a velocidade V 1 2 da expessão obtida no Passo 4:

p 2 - p 1 = ρ V 1 2 2 1 - D 1 2 D 2 2 2 - K

V 1 2 = 2 p 2 - p 1 ρ 1 - D 1 2 D 2 2 2 - K

Então, a velocidade na seção 1 é:

V q = 2 p 2 - p 1 ρ 1 - D 1 2 D 2 2 2 - K

Sabendo que:

p 2 - p 1 = ρ á g u a g ∆ h

A velocidade na seção 1 será:

V 1 = 2 ρ á g u a g ∆ h ρ a r 1 - D 1 2 D 2 2 2 - K

Passo 6

Sabendo que a relação de áreas A 1 / A 2 é dada por:

A 1 A 2 = π D 1 2 4 π D 2 2 4 = D 1 2 D 2 2

A 1 A 2 = 75 × 10 - 3 2 225 × 10 - 3 2 = 0,111

Então pela Figura 8.15 e conhecendo A 1 / A 2 = 0,111 , o coeficiente de perda de carga para a expansão vale:

K = 0,8

Passo 7

Então, a velocidade V 1 será:

V 1 = 2 ρ á g u a g ∆ h ρ a r 1 - D 1 2 D 2 2 2 - K

V 1 = 2 × 1000 × 9,81 × ( 5 × 10 - 3 ) 1,23 × 1 - 0,111 2 - 0,8

V 1 = 2 × 9,81 × ( 5 × 10 - 3 ) 1 - 0,111 2 - 0,8

V 1 = 20,6   m / s

Passo 8

A vazão será dada por:

Q = V 1 A 1

Q = V 1 π D 1 2 4

Q = 20,6 × π × 75 × 10 - 3 2 4

Q = 0,091 × 10 - 3   m 3 / s

Ou ainda:

Q = 91   L / s

Resposta

V 1 = 20,6   m / s

Q = 0,091 × 10 - 3   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento laminar completamente desenvolvido em um tubo circular. Se o diâmetro do tubo for reduzido pela metade enquanto a vazão e o comprimento do tubo forem mantidos constantes, a perd
Como o fator de atrito do escoamento em um tubo está relacionado à perda de pressão? Como a perda de pressão está relacionada ao requisito de potência de bombeamento para determinada vazão em massa?
Como a perda de carga está relacionada à perda de pressão? Para determinado fluido, explique como você converteria a perda de carga em perda de pressão.
O que é a viscosidade turbulenta? Pelo que ela é causada?
Explique por que o fator de atrito é independente do número de Reynolds para números de Reynolds muito grandes.