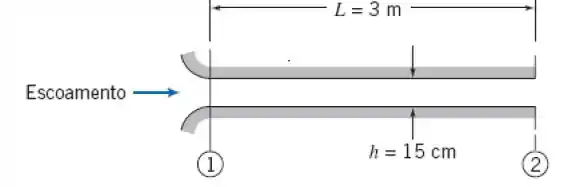
Ar de resfriamento é suprido através do canal largo e plano mostrado. Para o mínimo de ruído e perturbação do fluxo de saída, camadas limites laminares devem ser mantidas sobre as paredes do canal. Estime a máxima velocidade do escoamento na entrada para a qual o escoamento de saída será laminar. Considerando perfis de velocidade parabólicos nas camadas limite laminares, avalie a queda de pressão, Expresse a sua resposta em polegadas de água.
Passo 1
Listinha do que a gente precisa fazer:
- achar a velocidade máxima na entrada para o escoamento continuar laminar na saída
- achar em polegadas de água
Dados:
- altura do tubo:
- comprimento do tubo:
- considerando ar-padrão: e
- perfil parabólico:
Nesse perfil, vale que:
E a gente sabe que a escoamento deixa de ser laminar quando ultrapassa:
Vamos começar!
Passo 2
A gente tem que:
Precisamos que isso aconteça na saída do tubo. Então . Depois, substituindo os dados do problema e isolando , temos que:
Passo 3
Vamos precisar achar a variação de pressão, para isso a gente precisa da velocidade no fim do tubo. Vamos usar a conservação da massa:
Só que é área onde temos escoamento uniforme, ou seja, fora da camada limite. Então a gente pode escrever (sendo a largura do tubo):
Como o canal é largo, só consideramos camadas nas paredes de cima e de baixo.
Isolando :
Tá, mas quem é
Passo 4
A gente pode achar substituindo os dados do problema e aqui:
Achamos que:
Pela definição de para o perfil parabólico, a gente tira que:
Então:
Substituindo tudo o que a gente tem aqui:
Passo 5
Agora é só usar Bernoulli para achar a variação de pressão:
Transformando em polegadas de água:
Sabendo que , e substituindo os dados que a gente tem: