Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 72
Tabela 9.1 mostra os resultados numéricos extraídos da solução de Blasius para as equações da camada limite laminar. Trace o gráfico da distribuição de velocidade (note que, da Eq. 9.13, ). Sobre o mesmo gráfico, trace a distribuição de velocidade turbulenta dada pela expressão de potência da Eq. 9.24. Qual deles é mais provável de separar primeiro, quando encontrar um gradiente adverso de pressão? Para justificar sua resposta, compare os fluxos de quantidade de movimento destes perfis (os dados do perfil laminar podem ser integrados usando um método numérico tal como a regra de Simpson)
Passo 1
Precisamos traçar os gráficos dos perfis de velocidade juntos, e depois calcular o fluxo de quantidade de movimento para cada um e decidir a partir daí qual separaria primeiro.
Dados:
-Perfil laminar de Blasius:
-Perfil turbulento
É esperado que o perfil laminar separe primeiro, por ter conhecidamente menor fluxo comparado ao turbulento, mas vamos provar isso aí.
Vamos começar!
Passo 2
Para traçar os gráficos, vamos apenas plotar valores que satisfaçam nossas equações:
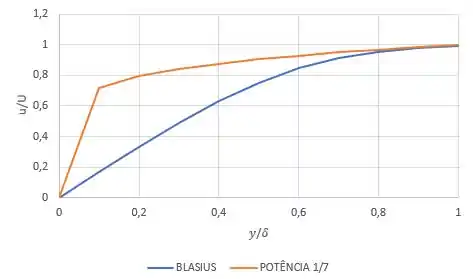
Passo 3
Calculando o fluxo para o perfil de Blasius
Vamos usar a substituição:
Podemos usar essa integração numérica de Simpson:
Onde é o valor de passos, e é o valor do passo.
Usando essa fórmulinha, e os dados do nosso gráfico de Blasius (podemos tirar os valores de e todos os outros que precisamos do gráfico):
Passo 4
Calculando o fluxo para o perfil de potência :
Logo, esse é o fluxo maior e, por isso, o caso laminar seria o primeiro a separar.
Passo 5
Logo, o fluxo do escoamento turbulento é maior e, por isso, o caso laminar seria o primeiro a separar.
Resposta
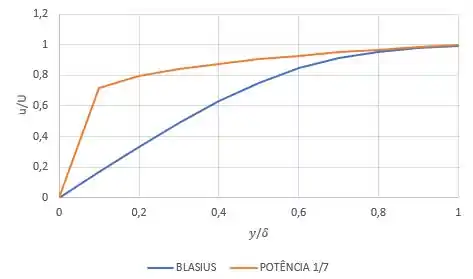
O caso de Blasius separaria primeiro por ter o fluxo menor.