Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 118
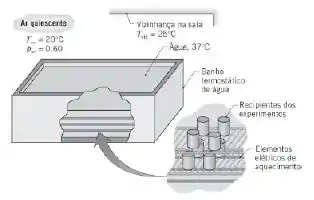
Um banho de água é usado para manter recipientes fechados contendo reações biológicas experimentais a uma temperatura uniforme de . A parte superior do banho tem largura e comprimento de e , respectivamente, e é descoberta para permitir fácil acesso para a remoção ou colocação dos recipientes. O banho está localizado em um laboratório sem correntes de ar, com o ar a pressão atmosférica, a uma temperatura de e com uma umidade relativa de . As paredes do laboratório estão a uma temperatura uniforme de .
a) Estime a perda térmica na superfície do banho por troca radiante com a vizinhança.
b) Calcule o número de Grashof usando a Equação 9.65, que pode ser usada em escoamentos de convecção natural impulsionados por gradientes de temperatura e de concentração. Use um comprimento característico que é apropriado para a superfície exposta do banho de água.
c) Estime o coeficiente de transferência de calor por convecção natural usando o resultado para obtido na parte (b).
d) Recorra à analogia entre as transferências de calor e de massa e use uma correlação apropriada para estimar o coeficiente de transferência de massa usando . Calcule a taxa de evaporação da água em base diária e a perda térmica por evaporação.
e) Calcule a perda de calor total na superfície e compare as contribuições relativas dos efeitos sensível, latente e radiante. Reveja as hipóteses feitas em sua análise, especialmente aquelas relacionadas à analogia termomássica.
Passo 1
Começamos o problema obtendo as seguintes a propriedade do vapor de água na Tabela sob a temperatura de :
Sob a temperatura :
Agora, na Tabela obtemos as seguintes propriedades do ar sob a temperatura de :
Sob a temperatura :
Calculando a temperatura de filme:
Na Tabela obtemos as seguintes propriedades do ar sob a temperatura de :
Na Tabela obtemos a seguinte propriedade sob a temperatura de :
Passo 2
Letra a)
Calculando o coeficiente de transferência de calor por radiação:
Dados:
;
;
.
Temos:
Calculando a taxa de transferência de calor por radiação:
Sendo:
.
Temos:
Passo 3
Letra b)
Calculando o número de Grashof:
Calculando a densidade da mistura na superfície:
Calculando a densidade do fluido inativo:
Calculando a densidade média do filme:
Voltando na equação de Grashof e com os seguintes dados:
;
.
Temos:
Passo 4
Letra c)
Calculando o número de Rayleigh:
Calculando o número médio de Nusselt:
Calculando o coeficiente médio de transferência de calor por convecção:
Passo 5
Letra d)
O número Rayleigh mássico se dá por:
Calculando o número de Schmidt:
Calculando o número Rayleigh mássico:
Calculando o número médio de Sherwood:
Calculando o coeficiente de transferência de massa:
Passo 6
Calculando a taxa de evaporação da água diariamente:
Passo 7
Calculando a perda de calor por evaporação:
Passo 8
Letra e)
Calculando a perda de calor por convecção:
Calculando a perda total de calor da superfície que deve ser fornecida como potência elétrica:
Desse modo, temos que as perdas de calor sensíveis são por convecção e radiação, e elas representam do total, enquanto o que sobre é a perda latente por evaporação, que equivale a aproximadamente .