Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 67
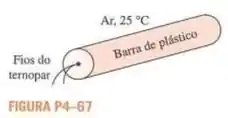
Uma barra de plástico de de diâmetro tem um termopar inserido para medir a temperatura no seu centro. A barra de plástico foi aquecida inicialmente a uma temperatura uniforme de e deixada para resfriar na temperatura do ar ambiente de . Após de resfriamento, o termopar mediu a temperatura no centro da barra como . Determine o coeficiente de transferência de calor por convecção desse processo.
Passo 1
Dados fornecidos no enunciado:
Densidade da barra de plástico:
Calor específico da barra de plástico:
Condutividade térmica da barra de plástico:
Diâmetro da barra de plástico:
Raio da barra de plástico:
Temperatura inicial da barra de plástico:
Temperatura do ar ambiente:
Temperatura final no centro da barra de plástico:
Tempo de resfriamento da barra de plástico:
Passo 2
Para determinar o coeficiente de transferência de calor por convecção desse processo, podemos usar o “Gráfico da temperatura transiente e da transferência de calor do cilindro longo de raio , inicialmente a uma temperatura uniforme , submetido à convecção em todos os lados para um meio a uma temperatura com coeficiente de convecção ”.
Para usá-lo, pisamos te o número de Fourier seja .
Vamos começar calculado a difusividade térmica que será usado no cálculo do número de Fourier.
A difusividade térmica da haste de plástico pode ser calculada da seguinte maneira:
Aqui, é a difusividade térmica da haste plástica, é a condutividade térmica da haste plástica, é a densidade da haste plástica e é o calor específico a pressão constante. Substituindo pelos dados fornecido, temos:
Passo 3
Com a difusividade térmica, podemos calcular o número de Fourier. Assim temos:
Aqui, é o número de Fourier, é o tempo necessário para o resfriamento e é o raio da haste de plástico. Substituindo os termos pelos valores conhecidos, temos:
O número de Fourier é maior que , assim podemos continuar com a análise do gráfico.
Passo 4
Para analisar o gráfico, vamos precisar primeiro calcular a relação de temperatura adimensional.
Aqui, é a temperatura no centro da barra de plástico, é a temperatura ambiente e é a temperatura inicial da barra de plástico. Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 5
Podemos obter o valor analisando o gráfico “ Temperatura na linha central” da Fig. 4-17.
Na Fig. 4-17, para e , O valor de encontrado é o seguinte:
Podemos calcular o coeficiente de transferência de calor por convecção usando a seguinte equação:
Aqui, o coeficiente de transferência de calor por convecção é . Substituindo os termos pelos dados conhecidos, temos:
Portanto, o coeficiente de transferência de calor por convecção é .