Exercícios de Método dos Parâmetros Concentrados - Lista de Exercícios Resolvida

Um armazenamento de energia térmica consiste em um grande canal retangular no qual é bem isolado em sua superfície externa e engloba camadas alternadas de material de armazenagem e canal de escoamento.

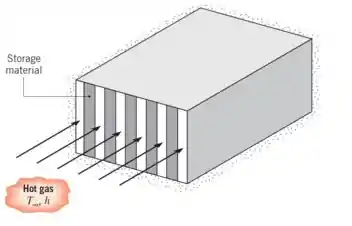
Cada camada do material de armazenamento é uma placa de alumínio () de largura , a qual está a uma temperatura de . Considere condições para as quais a unidade de armazenamento é carregada pela passagem de um gás quente através dos canais. A temperatura do gás e o coeficiente de convecção são considerados valores constantes de e em todo o canal.

Quanto tempo irá levar para atingir da energia armazenada máxima possível?

Qual será a temperatura do alumínio nesse instante?

Considere um paralelepípedo de cobre (, e ) com lados , inicialmente na temperatura uniforme de .

Este bloco de cobre é imerso em um fluido a . O coeficiente de transferência de calor entre o bloco e o fluido é de . Calcule:

Tempo necessário para que o ponto central do bloco seja resfriado até .

Taxa inicial de variação de temperatura .

Rejeitos radioativos são colocados em um recipiente esférico de parede delgada. Os rejeitos geram energia térmica por unidade de volume . O raio do recipiente é .

Assumindo que o recipiente está inicialmente a uma temperatura e sabendo que esse é colocado em um líquido inerte que se encontra a e que fornece um coeficiente convectivo uniforme.

Determine o comportamento da temperatura com o tempo no interior do recipiente.

Qual a temperatura do estado estacionário?

Determine a quantidade de calor trocada com o meio após atingir o estado estacionário.

Para todos os casos assuma modelo de parâmetros concentrados.

Expresse os resultados em termos de , , , , (condutividade térmica do rejeito), (massa específica) e (capacidade térmica do rejeito).

A medida que as estações espaciais permanentes aumentam de tamanho, existe um consequente aumento na quantidade de potência elétrica que elas dissipam. Para manter a temperatura nos compartimentos internos dentro de limites estabelecidos, torna-se necessário transferir o calor dissipados para o espaço.

Um novo sistema proposto para a dissipação de calor é conhecido por Radiador de Gotículas Líquidas. O calor é incialmente transferido para um óleo especial para alto vácuo, que é então injetado no espaço exterior em forma de uma corrente de pequenas gotículas. A corrente percorre uma distância , ao longo da qual se resfria pela irradiação de energia para o espaço exterior, que se encontra a uma temperatura absoluta igual a zero. As gotículas são, então, coletadas e retornadas para a estação espacial.

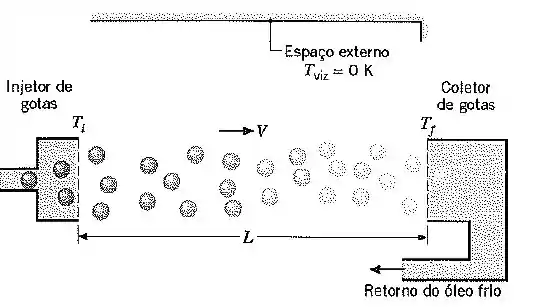
Considere condições nas quais as gotas, com emissividade e diâmetro , são injetadas no espaço a uma temperatura e a uma velocidade .

As propriedades do óleo são , e .

Supondo que cada gota irradia calor para o espaço externo a , determine a distância necessária para que as gotículas atinjam o coletor a uma temperatura final . Qual é a quantidade de energia térmica dissipada por cada gota?

Uma parede plana de um forno é fabricada de aço carbono (,, ) com espessura . A fim de proteger a parede dos efeitos da corrosão dos gases de combustão do forno, uma superfície da parede é revestida com um fino filme de cerâmica, para uma unidade de área superficial, tem uma resistência térmica de . A superfície oposta é bem isolada do ambiente.

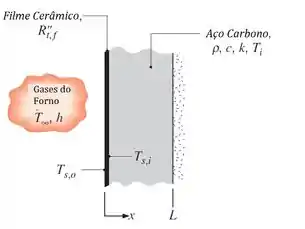
Quando o forno entra em operação, a parede encontra-se a uma temperatura inicial de e os gases de combustão a entram no forno, promovendo um coeficiente de convecção de no filme cerâmico.

Considerando que a capacidade térmica do filme é desprezível, quanto tempo levará para a superfície interna do aço atingir a temperatura de ?

Qual é a temperatura da superfície exposta do filme cerâmico nesse instante?

Uma esfera de aço , , de de diâmetro está inicialmente a temperatura uniforme igual a . A esfera é subitamente colocada num ambiente mantido a .

Faça um balanço de calor na esfera e obtenha a equação de conservação de energia, justificando as suas hipóteses. Calcule o tempo requerido para a esfera atingir , considerando que o coeficiente convectivo de troca de calor vale .

(Adaptada) Uma junção termopar, que pode ser aproximada como uma esfera, deve ser utilizada para a medida de temperatura em uma corrente de gás. O coeficiente de convecção entre a superfície da junção e o gás é e as propriedades termofísicas da junção são , e .

Determine o diâmetro da junção necessário para que o termopar tenha uma constante de tempo de .

Se a junção encontra-se a e é colocada em uma corrente de gás a , quanto tempo levará para que a junção alcance ?

Considere agora que também há troca de calor por radiação entre as paredes de um duto que circunda a corrente do gás. Se as paredes do duto encontram-se a e a emissividade do termopar é , calcule a temperatura do regime estacionário e determine a equação diferencial proveniente do balanço de energia transiente.

Um arame longo de diâmetro é imerso em um banho de óleo à temperatura de . O arame possui uma resistência elétrica por unidade de comprimento de . A corrente que flui através do arame vale , o coeficiente de convecção é e as propriedades do arame são ,, .

Qual é a temperatura em regime estacionário do arame?

A partir do tempo em que a corrente é aplicada, quanto tempo levará para o arame atingir uma temperatura que não exceda do valor do regime estacionário?

O coeficiente de transferência de calor para o ar escoando sobre uma esfera deve ser determinado pela observação do comportamento dinâmico da temperatura de uma esfera, que é fabricada em cobre puro.

A esfera, que possui de diâmetro, encontra-se a antes de ser inserida em uma corrente de ar que tem a temperatura de . Um termopar sobre a superfície externa da esfera indica após da inserção da esfera na corrente de ar.

Admita que a esfera se comporta como um objeto espacialmente isotérmico e calcule o coeficiente de transferência de calor.

Dados: , ,

Uma esfera sólida de aço () de de diâmetro é revestida com uma camada de material dielétrico de espessura e condutividade térmica . A esfera revestida está inicialmente a uma temperatura de e é subitamente resfriada em um grande banho de óleo, o qual se encontra a e . Estime o tempo necessário para que a temperatura da esfera revestida atinja .

Dica: despreze o efeito do armazenamento de energia no material dielétrico, uma vez que sua capacidade térmica () é pequena quando comparada com a da esfera de aço.

Eixos de aço carbono (AISI 1010) com de diâmetro são tratados termicamente pelo aquecimento em fornalhas a gás onde os gases se encontram a e mantêm um coeficiente convectivo de .

Se os eixos entram no forno a , quanto tempo eles devem permanecer no interior da fornalha para suas linhas de centro atingirem a temperatura de ?

Dados: , , , .