Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 46
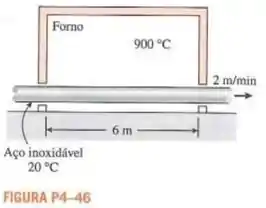
Barras cilíndricas longas de aço inoxidável AISI de de diâmetro são tratadas termicamente passando à velocidade de por um forno de de comprimento mantido a . O coeficiente de transferência de calor no forno é . Considerando que as barras entram na estufa a , determine a temperatura na linha do centro quando saem.
Passo 1
Dador fornecidos no enunciado:
Diâmetro da barra cilíndrica:
Condutividade térmica do aço inoxidável:
Difusividade térmica do aço inoxidável:
Coeficiente de transferência de calor:
Temperatura do forno:
A temperatura inicial:
Comprimento do forno:
Velocidade da barra no forno:
Premissas:
As hastes cilíndricas de aço longas são tratadas termicamente em um forno.
A condução de calor nas hastes é unidimensional, pois as hastes são longas e possuem simetria térmica na linha central.
O coeficiente de transferência de calor é constante e uniforme em toda a superfície.
O número de Fourier é , para que as soluções aproximadas de um termo sejam aplicáveis.
Passo 2
Primeiramente vamos encontrar o tempo que a barra de aço permanece no forno usando a seguinte equação:
Aqui, é o comprimento do forno, é a velocidade da barra de aço passando pelo forno. Substituindo pelos dados fornecidos, temos:
Passo 3
Agora, vamos encontrar o número de Fourier usando a seguinte expressão:
Substituindo pelos dados fornecidos, temos:
Aqui, o Fourier é maior que , portanto, as soluções aproximadas de termo único são aplicáveis.
Passo 4
Podemos encontrar o número do Biot usando a seguinte expressão:
Aqui, é o coeficiente de transferência de calor e é a condutividade térmica da barra. Substituindo pelos dados fornecidos, temos:
Passo 5
Obtenha as constantes e correspondentes a este número Biot na tabela "Coeficientes utilizados na solução aproximada do termo da condução de calor transiente unidimensional em cilindros, Tabela 4-2". Usando interpolação, temos:
Passo 6
Agora, podemos então usar a solução para condução transiente unidimensional em um cilindro de raio submetido à condução em todas as superfícies. Devido estamos interessado na temperatura na linha central do cilindro, podemos usar a seguinte equação:
Substituindo os valores fornecidos e encontrados nos passos anteriores, temos:
Portanto, a temperatura da linha central da barra quando sai do forno é .