Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 30
Considere o sistema do Problema 5.1, no qual, durante o processo transiente, a temperatura na placa é isotérmica em relação às coordenadas espaciais.
(a) Obtenha uma expressão para a temperatura da placa em função do tempo em termos de , , e das propriedades da placa e .
(b) Determine a constante de tempo térmica e a temperatura do regime estacionário para uma placa em puro cobre com espessura de , quando , e . Estime o tempo necessário para o sistema atingir as condições de regime estacionário.
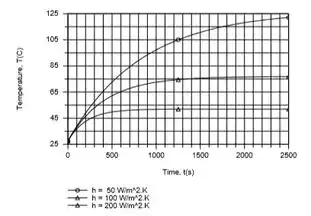
(c) Para as condições da parte (b), bem como para e calcule e represente graficamente os correspondentes históricos da temperatura da placa durante o intervalo .
Passo 1
Vamo lá galera! (a) Após a análise da seção 5.3, a necessidade de conservação de energia para o sistema é
Rearranjando, e com e ,
Definindo,
Com
A EDO formada é,
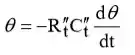
Passo 2
Separação de variáveis e integração,
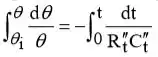
daí decorre que
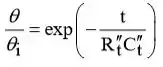
(b) Para , a temperatura em estado estacionário pode ser determinada com ; ou seja,
Para estimar o tempo para alcançar o estado estável, primeiro determine a constante de tempo térmica do sistema,
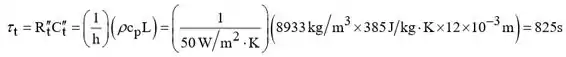
Com ,
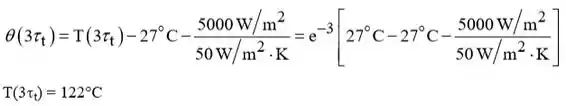
Passo 3
(c) Como mostram os resultados gráficos a seguir, que foram gerados usando o Modelo de Capacitância de IHT Lumped, a temperatura em estado estacionário e o tempo para alcançar o estado estacionário ambos diminuem com o aumento do
