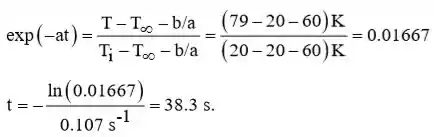Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 27
Um circuito integrado (chip), que tem L = 5 mm de lado e espessura , é encaixado em um substrato cerâmico. Sua superfície exposta é resfriada por convecção por um líquido dielétrico com e .
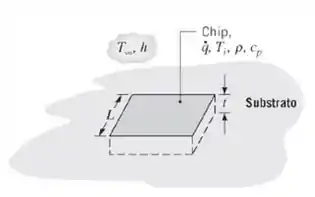
Quando desligado, o chip encontra-se em equilíbrio térmico com o refrigerante Contudo, quando o chip é energizado, sua temperatura aumenta até que uma nova condição de regime estacionário seja alcançada. Na análise a seguir, o chip energizado é caracterizado por um aquecimento volumétrico uniforme com . Supondo uma resistência de contato infinita entre o chip e o substrato, e uma resistência condutiva no interior do chip desprezível, determine a temperatura do chip no regime estacionário, . Após a ativação do chip, quanto tempo ele leva para atingir uma temperatura inferior à temperatura do regime estacionário? A massa específica e o calor específico do chip são e respectivamente.
Passo 1
Vamo lá galera! Em estado estacionário, a conservação de rendimentos energéticos nos leva a:
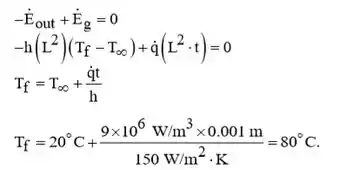
Passo 2
A partir da análise da capacidade geral, a Equação 5.15 reduz para
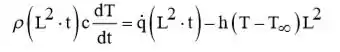
Com,
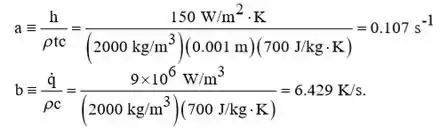
Passo 3
Por fim, Da Equação 5.24,
