Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 46

Um bloco cúbico de massa 10   k g e de aresta de 250   m m é puxado para cima em uma superfície inclinada, sobre o qual há um filme de óleo SAE 10W-30 a -1,1°C de espessura 0,025   m m . Determine a velocidade constante do bloco se ele for liberado. Se uma força de 75   N for aplicada para puxar o bloco para cima da superfície inclinada, determine a velocidade constante de subida do bloco. Se agora a força for aplicada para puxar o bloco para baixo, determine a velocidade constante do bloco. Considere que a distribuição de velocidade do bloco no filme seja linear. A superfície está inclinada de 30 ° a partir da horizontal.

Passo 1

Desenhando o diagrama de corpo livre sem a ação das forças puxando o bloco para cima e empurrando para baixo, temos:

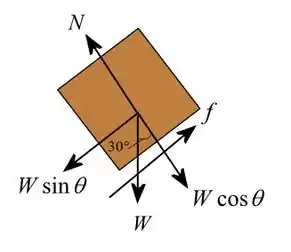
Passo 2

Analisando o diagrama, temos que a soma das forças atuando em x é igual a zero.

∑ F x = m ⋅ a x = 0

Assim:

F - f - W ⋅ s e n   θ = 0

Sendo:

F = F o r ç a   a p l i c a d a   n o   b l o c o ;

f = F o r ç a   d e   a t r i t o ;

W = F o r ç a   p e s o .

Passo 3

Sabemos que:

f = τ x y ⋅ A

Pela definição da Tensão de Cisalhamento, temos:

τ x y = μ d u d y = μ ⋅ u d

Então:

f = μ ⋅ u d ⋅ A = μ ⋅ u d ⋅ L 2

Passo 4

Determinando a velocidade constante do bloco se ele for liberado:

Sendo:

μ ( Ó l e o   S A E   10 W - 30 ,   - 1,1 ° C ) = 0,1   N / m 2 ;

F = 0   N ;

d = 2,5 x 10 - 5   m ;

L = 0,25   m ;

W = - m ⋅ g = 10 ⋅ 9,8 = - 98   N ;

θ = 30 ° .

Assim, temos:

F = μ ⋅ u d ⋅ L 2 + W ⋅ s e n   θ

0 = 0,1 ⋅ u 1 2,5 x 10 - 5 ⋅ 0,25 2 - 98 ⋅ s e n   30 °

u 1 = 98 ⋅ s e n   30 ° ⋅ 2,5 x 10 - 5 0,1 ⋅ 0,25 2 = 0,196   m / s

Passo 5

Se uma força de 75   N for aplicada para puxar o bloco para cima da superfície inclinada, determine a velocidade constante de subida do bloco.

Aqui, utilizaremos os mesmos dados do Passo 4, sendo que F = 75   N .

F = μ ⋅ u d ⋅ L 2 + W ⋅ s e n   θ

75 = 0,1 ⋅ u 2 2,5 x 10 - 5 ⋅ 0,25 2 + 98 ⋅ s e n   30 °

u 2 = 75 - 98 ⋅ s e n   30 ° ⋅ 2,5 x 10 - 5 0,1 ⋅ 0,25 2 = 0 , 104   m / s

Passo 6

Se agora a força for aplicada para puxar o bloco para baixo, determine a velocidade constante do bloco.

Utilizaremos os mesmos dados do Passo 4, sendo que F = - 75   N .

F = μ ⋅ u d ⋅ L 2 + W ⋅ s e n   θ

- 75 = 0,1 ⋅ u 3 2,5 x 10 - 5 ⋅ 0,25 2 + 98 ⋅ s e n   30 °

u 3 = - 75 - 98 ⋅ s e n   30 ° ⋅ 2,5 x 10 - 5 0,1 ⋅ 0,25 2 = 0 , 496   m / s

Resposta

u 1 = 0,196   m / s

u 2 = 0,104   m / s

u 3 = 0,496   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um parâmetro que é frequentemente usado para descrever o desempenho de bombas é a velocidade específica, N s , dada por: N s = N r p m Q g p m 1 2 H f t 3 4 Quais são as unidades da velocidade específ
ExpresseosseguintesvaloresemunidadesGB: 180 c c / m i n 300 k W h 50 N s / m ² ² 40 m ²h r ²
Expresse os seguintes valores em unidades SI: 100 cfm (ft³/min) 5 gal 65 mph 5,4 acres
Deduza os seguintes fatores de conversão:Converta um calor específico de 4,18 k J / k g K para B t u / l b m R . Converta uma velocidade de 30 m / s para m p h . Converta um volume de 5,0 L para in³
O livre caminho médio λ de uma molécula de gás é a distância média que ela percorre antes de colidir com outra molécula. Ele é dado por: γ = C m ρ d 2 Em que m e d são a massa da molécula e o diâmetro