Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas Abrangentes - Ex. 1

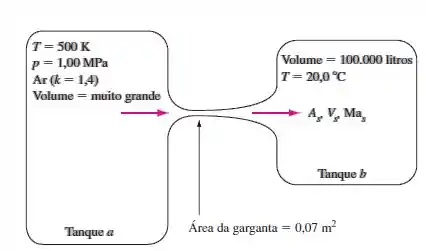
O bocal convergente-divergente esboçado na figura abaixo é projetado para um número de Mach de 2,00 no plano de saída (admitindo-se que o escoamento permaneça aproximadamente isentrópico). O escoamento vai do tanque “a” para o tanque “b”, e o tanque “a” é muito maior que o tanque “b”. (a) Determine a área de saída A s e a contrapressão p c que permitirão que o sistema opere nas condições de projeto (b). Com o passar do tempo, a contrapressão aumentará, uma vez que o segundo tanque lentamente se enche com mais ar. Todavia, visto que o tanque “a” é muito grande, o escoamento no bocal permanecerá o mesmo, até que uma onda de choque normal apareça no plano de saída. Em qual contrapressão isso ocorrerá? (c) Se o tanque “b” é mantido a temperatura constante T = 20 ° C , calcule quanto tempo levará para o escoamento ir das condições de projeto para as condições da parte (b), isto é, com uma onda de choque no plano de saída?

Passo 1

Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Bem, na letra (a) vai ser bem tranquilo da gente calcular as coisas, por que?

Bem, se ele falou pra gente qual deve ser o número de Mach na saída, a gente consegue ir na nossa tabela B.1 do livro e pegar os valores das relações entre pressões e área, se liga!!

Para Mach 2,0, na tabela B.1 a gente vai ter que:

p s p o = 0,1278 → p s = 0,1278 p o

Onde p o = 1 M p a = 10 6 P a

p s = 0,1278 10 6 = 128000   P a

A s A * = 1,6875

Onde A * = 0,07   m ² , logo A s = 1,6875 0,07 = 0,118   m ²

Passo 2

(b) Vamos agora calcular a razão de pressão através de um choque com Mach = 2,0:

M a s = 2,0

De acordo com a tabela B.2 do livro, a relação entre as pressões será dada por:

p b p e = 4,5 → p b = 4,5 128000 = 575000 P a

Passo 3

(c) Calculamos agora o valor da vazão mássica e depois qual deve ser esse “delta” mássico que devemos ter no tanque, se liga!!!

m ˙ = m ˙ m á x = 0,6847 p o A * R T

Para o ar, temos que R = 287   m 2 / s ² . K

m ˙ = m ˙ m á x = 0,6847 10 6 0,07 287 500 = 126 k g s

Logo a variação de massa que vamos ter no nosso tanque é de:

Δ m t a n q u e = ρ f i n a l - ρ i n i c i a l V t a n q u e = p b R T b - p s R T s V t a n q u u e

Δ m t a n q u e = 575000 287 293 - 128000 287 293 100 = 531 ,   9   k g

Bem, considerando que a vazão mássica é constante, o tempo requisitado é simplesmente a razão dessas duas quantidades que encontramos, certo?

Δ t = Δ m t a n q u e m ˙ = 531,9 126,5 = 4,2   s

Resposta

  1. p s = 128   k P a A s = 0,118   m ²
  2. p b = 575   k P a
  3. Δ t = 4,2   s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pneu de automóvel ao nível do mar está inicialmente a 220,6 kPa de pressão manométrica e 24 o C . Quando ele é perfurado com um furo que se assemelha a um bocal convergente, sua pressão cai para 10
Um tanque de suprimento a 500 kPa e 400 K fornece ar a um bocal convergente-divergente cuja área da garganta é de 9 cm². A área de saída é de 46 cm². Estabeleça as condições no bocal se a pressão exte
A hipótese de gás perfeito conduz tranquilamente às relações de números de Mach que são muito úteis (e tabeladas). O mesmo não ocorre para gases reais como o vapor. Para ilustrar, admita que o vapor a
Ar a 500 K escoa através de um bocal convergente-divergente com área de garganta de 1 cm² e área de saída de 2,7 cm². Quando a vazão em massa é de 182,2 kg/h, uma sonda de Pitot estática colocada no p
Ar escoa isentropicamente em um bocal convergentedivergente com uma garganta de 3 cm² de área. Na seção 1, a pressão é de 101 kPa, a temperatura é de 300 K e a velocidade é de 868 m/s. (a) O bocal est