Enunciado
Física - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 147
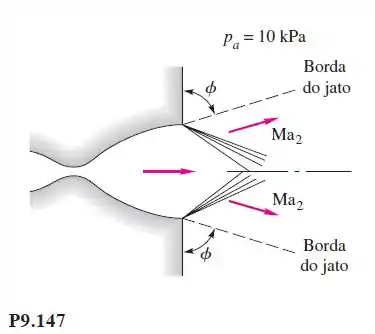
Um bocal convergente-divergente com razão de área de saída 4:1 e 500 kPa, como na Figura P9.147, opera em uma condição subexpandida (caso I da Figura 9.12b). A pressão do recipiente é 10 kPa, que é menor que a pressão de saída, de modo que ondas de expansão se formam para fora da saída. Para as condições dadas, qual será o número de Mach e o ângulo da borda do jato? Como de costume, admita k = 1,4.
Passo 1
Bora pra mais uma!
Vamos encontrar o numero de Mach na saída e então executar a expansão de Prandtl-Meyer:
Sendo obtemos o numero de Mach e então :
Portanto, Note que é igual à .
Resposta
Exercícios de Livros Relacionados
Admita que a água segue a equação 1.19 com n = 7 e B = 3000. Calcule o módulo de elasticidade volumétrica (em kPa) e a velocidade do som (m/s) a (a) 1 atm e (b) 1100 atm (a parte mais profunda do ocea
A 300°C e 1 atm, calcule a velocidade do som do (a) nitrogênio, (b) hidrogênio, (c) hélio, (d) vapor e (e) U F 6 238 ( k ≈ 1,06 )
Os carros de corrida na pista de Indianápolis atingem velocidades médias de 296 km/h. Após determinar a altitude de Indianápolis, encontre o número de Mach desses carros e avalia se a compressibilidad
Um submarino a uma profundidade de 800 m envia um sinal de sonar e recebe de volta a onda refletida de um objeto similar em 15 s. Utilizando o Problema 9.12 como orientação, calcule a distância até o
Em 1976, o SR-71A, voando a 20 km de altitude padrão, estabeleceu uma velocidade recorde de 3326 km/h para um avião a jato. Avalie a temperatura, em °C, em seu ponto de estagnação frontal. Para qual n