Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 56
Uma bomba centrífuga está instalada em um sistema de tubulações de ferro fundido com e . A superfície do reservatório a montante da bomba está abaixo do reservatório a jusante. Determine e trace a curva de altura de carga do sistema. Determine a vazão volumétrica (valor e sentido) através do sistema, quando a bomba não estiver operando. Estime a perda de carga por atrito, a potência requerida e o custo horário de energia para elevar água a através desse sistema.
Passo 1
Considerações:
- Escoamento Estacionário;
- Fluído Incompressível;
- (reservatório muito grande);
- ;
- ;
- .
Passo 2
Escreva a Equação de Bernoulli:
Fazendo as considerações do Passo 1:
Sendo:
Temos que:
Passo 3
Calculando:
Sendo:
.
.
Temos:
Passo 4
Do Número de Reynolds:
Sendo:
(Tabela A.7);
.
Temos:
Obtendo :
Com tabelado para Ferro Fundido igual a .
Com o Diagrama de Moody, obtemos os seguintes valores para :
Passo 5
Voltando na equação do Passo 2:
Sendo:
;
;
;
;
Temos:
Passo 6
Repetindo os cálculos para diferentes vazões, temos:
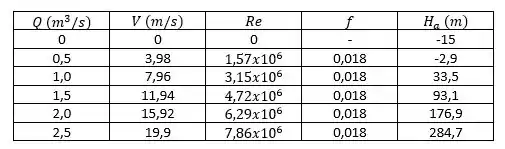
Plote o gráfico:
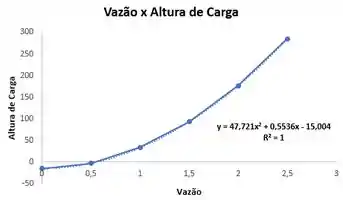
Pela equação obtida do gráfico, temo:
Determinando a vazão volumétrica através do sistema, quando a bomba não estiver operando.
Quando a potência de entrada é zero, a altura de carga também é igual à zero.
Passo 7
Estimando a perda de carga por atrito.
Passo 8
Calculando a potência da bomba.
Não há informações sobre a velocidade.
Assim, assumindo a eficiência da bomba para a vazão de , e analisando a Figura 10.9.
Temos uma eficiência de .
Então:
Passo 9
Custo horário de energia elétrica, admitindo que a energia elétrica custe por e que a eficiência do motor elétrico seja igual a .