Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 86

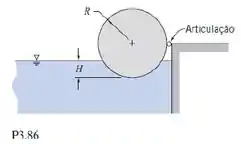
O cilindro mostrado é suportado por um líquido incompressível de massa específica ρ , e é articulado ao longo do seu comprimento. O cilindro, de massa M , comprimento L e raio R , está imerso no líquido até uma profundidade H . Obtenha uma expressão geral para a densidade relativa do cilindro em função da razão entre a profundidade no líquido e o raio do cilindro, α   =   H / R , necessária para manter o cilindro em equilíbrio para 0   ≤   α   ≤   1 . Trace um gráfico com os resultados.

Passo 1

Nessa questão temos cilindro que é articulado ao longo de seu comprimento e imerso em um líquido incompressível até a profundidade. Devemos encontrar uma expressão para a gravidade específica do cilindro em função de α = H   /   R necessária para manter

o cilindro em equilíbrio para α variando de   0 a 1 .

Agora vamos ver com quais expressões podemos calcular isso:

d p d h = ρ g , pressão hidrostática onde h é positivo para a superfície livre.

F v = ∫ p d A y , força hidrostática vertical

∑ M = 0 , equilibrio rotacional

Como todo problema da MecFLu, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando na superfície.

Passo 2

Inicialmente precisamos analisar que deve haver um equilíbrio entre os momentos devido a força hidrostática e o peso do cilindro. Logo, vamos integrar a formula da pressão hidrostática:

d F v = d F cos ⁡ θ = p   d A cos ⁡ θ = ρ g h w R   d θ cos ⁡ θ

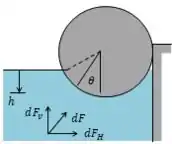
Para a profundidade quando o cilindro está submerso, temos: h = H - R ( 1 - cos ⁡ θ ) , então, a força vertical fica:

d F v = ρ g H - R 1 - cos ⁡ θ w R   cos ⁡ θ d θ

d F v = ρ g w R 2 H R - 1 - cos ⁡ θ cos ⁡ θ d θ

Como α   =   H / R , então

d F v = ρ g w R 2 α - 1 cos ⁡ θ + cos ⁡ θ 2 d θ

Usando a propriedade do cosseno:

d F v = ρ g w R 2 α - 1 cos ⁡ θ + 1 + cos ⁡ 2 θ 2 d θ

Passo 3

Nesse passo vamos aplicar a integração. Quando α não for maior que 1, a força hidrostática horizontal será zero devido à simetria, e a força vertical é:

F v = ∫ - θ m a x θ m a x 1 d F v = ∫ 0 θ m a x 2 d F v

Para o cos ⁡ θ m a x , temos: cos ⁡ θ m a x = R - H R = 1 - α , oou melhor, θ m a x = acos ⁡ ( 1 - α ) .

Substituindo tudo isso na expressão do passo 2:

F v = 2 ρ g w R 2 ∫ 0 θ m a x α - 1 cos ⁡ θ + 1 2 + 1 2 cos ⁡ 2 θ d θ

Logo,

F v = ρ g w R 2 acos ⁡ 1 - α - 1 - α α 2 - α

Passo 4

A linha de ação da força vertical devida ao líquido é através do centróide do líquido deslocado, isto é, através do centro do cilindro.

Assim, o peso do cilindro é dado por:

W = m g = ρ c V g = S G ρ π R 2 w g

onde ρ é a densidade do fluido e S G = ρ c ρ .

A linha de ação do peso também passa pelo centro do cilindro. Tomando um momento sobre a dobradiça que obtemos:

∑ M = W R - F v R = 0

Ou:

W = F v

Portanto,

S G ρ π R 2 w g = ρ g w R 2 acos ⁡ 1 - α - 1 - α α 2 - α

S G = 1 π acos ⁡ 1 - α - 1 - α α 2 - α

E, por fim, traçamos o gráfico de resultados, que vai ter a seguinte cara:

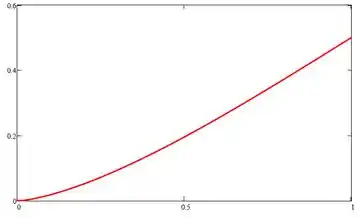
Prontinho!!

Resposta

S G = 1 π acos ⁡ 1 - α - 1 - α α 2 - α

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra uniforme de madeira (d = 0,65) tem 10 cm por 10 cm por 3 m e está articulada em A, como mostra a Figura P2.120. A que ângulo theta a barra flutuará em água a 20°C?
Um malandro colocou óleo, de densidade do, no ramo esquerdo do manômetro da figura abaixo. Não obstante, o tubo em U ainda é útil como um dispositivo de medida de pressão. Ele é ligado a um reservatór
A solid sphere, of diameter 18 cm, fl oats in 208C waterwith 1527 cubic centimeters exposed above the surface.(a) What are the weight and specifi c gravity of this sphere?(b) Will it fl oat in 208C ga
The bathysphere of the chapter-opener photo is steel,SG
The 2-in by 2-in by 12-ft spar buoy from Fig. P2.113 has5 lbm of steel attached and has gone aground on a rock, asin Fig. P2.115. Compute the angle θ at which the buoy willlean, assuming that the rock