O coeficiente de transferência de calor por convecção natural sobre uma chapa quente, fina e na posição vertical, suspensa no ar em repouso, pode ser determinado através da observação da variação da temperatura da chapa com o tempo, na medida em que ela esfria. Considerando a placa isotérmica e que a troca de calor por radiação com a vizinhança seja desprezível, determine o coeficiente de convecção no instante de tempo no qual a temperatura da chapa é de e a sua taxa de variação com o tempo é de . A temperatura do ar ambiente é de , a chapa mede, possui massa de , com um calor específico de .
Passo 1
A questão nos fala que temos uma placa vertical quente suspensa em ar frio parado e que ocorre uma mudança na temperatura da placa com o tempo no instante em que a temperatura da placa é de . Esquematicamente temos:
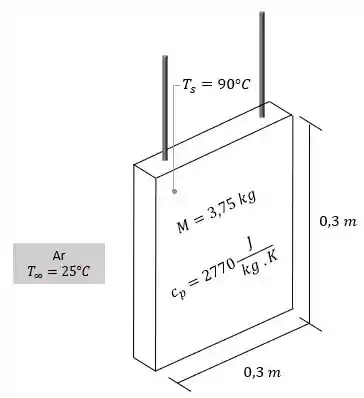
E nos pede para determinar o coeficiente de convecção no instante de tempo no qual a temperatura da chapa é de .
Passo 2
Para resolver essa questão vamos precisar fazer três considerações:
- A chapa é isotérmica, ou seja, a temperatura é uniforme em toda a sua extensão;
- A troca de radiação com o ambiente é desprezível;
- O calor perdido pelos fios de suspensão é desprezível.
Show! Agora considerando esses tópicos vemos que graficamente temos:
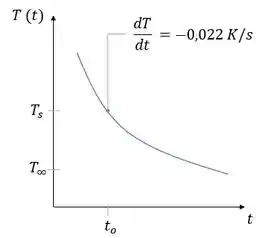
Como mostrado na curva de resfriamento acima, a temperatura da placa diminui com o tempo e a condição de interesse é por tempo. Para uma superfície de controle sobre a placa, a conservação de energia é:
Onde é a área superficial de um lado da placa.
Passo 3
Isolando o coeficiente de transferência de calor, nós ficamos com:
Substituindo os valores fornecidos pela questão,