Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 22
Calcule o valor do coeficiente de transferência de calor médio para a placa do Problema 7.21 quando a placa inteira é rodada de 90°, de modo que metade da aresta frontal fica constituída pela porção lisa (A) e a outra metade pela porção rugosa (B).
Passo 1
Esta questão é bem semelhante a questão 7.21, a grande mudança está na geometria da placa. Ao deixarmos a placa na vertical, teremos o seguinte caso:
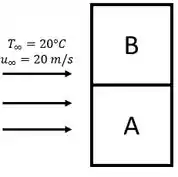
Um detalhe que a gente não precisa se preocupar é a placa que está acima (ou abaixo). O que importa é que as duas estão na vertical.
Agora, muito cuidado nesta hora!!! É sempre importante começarmos estas questões com as nossas hipóteses para o problema. Neste caso, temos regime permanente, propriedades constantes do ar e escoamento turbulento na parte rugosa.
Além disto, vamos aproveitar para calcular as propriedades do ar (o fluido que escoa), que está a 1 atm e a temperatura do filme (média da temperatura do ar com a temperatura da superfície) é .
Utilizando a tabela , temos: , , . Detalhe que obtivemos todos os dados a partir da interpolação da tabela.
Passo 2
Agora que entendemos o que estamos sujeitos, podemos partir para o cálculo do coeficiente de transferência de calor médio, o . Ele será dado pela média dos coeficientes médios da parte A e parte B. Logo,
Nosso trabalho então será calcular cada um deles.
Bom, para podermos calcular os coeficientes médios de transferência de calor, precisamos saber qual a correlação correta para o número de Nusselt.
Para respondermos esta pergunta, vamos calcular o número de Reynolds na parte A para saber se temos um escoamento laminar ou turbulento. Portanto,
Como o número de Reynolds foi próximo de , temos escoamento laminar por quase toda a parte A.
Então, como temos uma parte de escoamento laminar na parte A e escoamento turbulento na parte B, vamos utilizar a correlação do número de Nusselt para escoamento misto.
Passo 3
Para finalizar, começaremos o cálculo dos coeficientes médios de transferência de calor para a partir da parte A. Então, temos:
Já para a parte B, temos:
Portanto, o coeficiente médio em toda a placa é: