Considere o aparelho fotovoltaico concentrador do Problema 7.19. O aparelho deve ser instalado em um ambiente desértico, de modo que o espaço entre as lentes concentradoras e o topo da célula fotovoltaica é fechado para proteger a célula da abrasão por areia em condições de ventos. Como o resfriamento por convecção no topo da célula é reduzido pelo envoltório, um engenheiro propõe resfriar a célula fotovoltaica através da fixação de um dissipador de calor de alumínio na sua superfície inferior. As dimensões do dissipador de calor e o material são os mesmos do Problema 7.29. Há uma resistência de contato de na interface célula/dissipador de calor e um líquido dielétrico escoa entre as aletas do dissipador com e .

1. Determine a potência elétrica produzida pela célula fotovoltaica e a temperatura do silício para uma lente concentradora quadrada com .
2. Compare as potências elétricas produzidas pela célula com o dissipador de calor no lugar e com a superfície inferior resfriada diretamente pelo fluido dielétrico (isto é, sem o dissipador) para .
3. Determine a potência elétrica produzida e a temperatura do silício na faixa com o dissipador de alumínio no lugar.

Então, nosso trabalho seria descobrir esse , para a letra a), por exemplo. E como faríamos isto? Bom, vamos trabalhar com a analogia de circuitos térmicos, utilizando os circuitos desenvolvidos nas questões 7.19 e 7.29.

Com isto, temos:

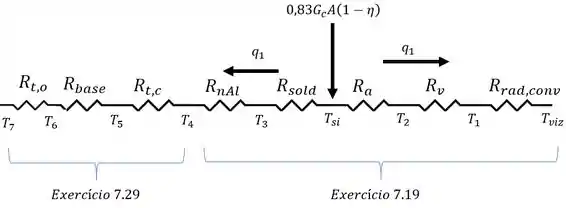
Então, temos que calcular cada um dos elementos. Começando pelos “mais fáceis”, isto é, deixando a aleta por último, temos:

Tenham sempre cuidado na hora de calcular a resistência térmica de convecção e radiação. A temperatura deve estar em Kelvin!

OBS: Todas as informações sobre as propriedades acima foram retiradas lá da questão 7.19.

Vamos calcular agora a resistência térmica devido a aleta, que é um pouco mais trabalhosa.

E como será dado a sua resistência térmica? Ela será dada pela seguinte relação:

Eita. São tantos termos que assusta ainda mais. Mas não se assustem, vamos destrinchar cada um dos termos.

A começar, temos a constante , que corresponde ao número de aletas. Portanto, . A constante é a área superficial das aletas em contato com o ar. Portanto, ele será expresso por:

E quem é a constante ? É a soma da área superficial de todas as aletas com a área da base em contato com o ar. Portanto,

E o termo ? Ela é a eficiência da aleta. Considerando que temos uma aleta plana retangular, a relação correta é . Mas, para calcularmos, vamos precisar do coeficiente de transferência de calor (e também é uma das constantes da fórmula de resistência térmica).

Calculando o número de Reynolds, temos:

Portanto, como , temos escoamento laminar. Então, a relação que devemos utilizar é:

Portanto, o coeficiente de transferência de calor será:

Pronto! Agora, realmente só falta a eficiência . Calculando o coeficiente , temos:

E o comprimento característico . Portanto,

Então, a resistência térmica será:

Muito trabalho né? Percebam que não são contas “muito difíceis”. O que confunde é a quantidade de relações que devemos utilizar.

Bom, agora, já temos quase todas as informações necessárias para descobrir a temperatura do silício e a potência do silício.

O que devemos fazer agora é obter equações que relacionem estas variáveis de alguma forma. E para isto, vamos começar fazendo um balanço de energia.

Lá do circuito de resistências térmicas, realizando um balanço de energia, temos:

Mas quem é e ? Novamente, analisando a taxa de transferência de calor, temos:

Já para o , temos:

Só que está em função de ,e não , podemos relacionar ambas as temperaturas também através da própria taxa através da seguinte relação:

E, para finalizar o sistema que temos de resolver, temos a equação desenvolvida lá na questão 7.19 que correlaciona com a temperatura do silício, a qual era:

Então, se a gente substitui as relações na nossa equação inicial, temos:

Se resolvermos a equação acima juntamente da seguinte equação:

Vamos obter um valor aproximado de . Este é um sistema bem complexo de resolver, necessitando de softwares que nos ajude.

Continuando, o termo será dado por:

E assim, concluímos que a potência será:

Para quem sofreu na letra a), a letra b) é uma moleza! Vamos primeiro resolver o sistema mantendo todas as características das nossas equações. A diferença será no valor , que deverá ser igual a 1500 mm agora.

Então, se a gente pega o sistema da questão anterior e resolve para o valor de , vamos obter os valores aproximados de e .

Basicamente, o que tivemos foi trabalho de cálculo apenas.

Agora, o “problema” é quando modificamos a questão. Se, ao invés de na parte inferior termos o dispositivo aletado da questão 7.29, colocarmos diretamente o fluido dielétrico?

Bom, o que nós precisamos fazer aqui são pequenas alterações. No lugar de , e , vamos substituir estas três resistências por apenas uma, devido a convecção. Ela será:

Notem que o coeficiente de transferência de calor nós já calculamos durante a parte da aleta.

Então, o cálculo do novo será:

E o sistema que devemos resolver é:

Resolvendo as duas equações acima, vamos obter . Substituindo este valor para o cálculo do e da potência, temos .