Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 87

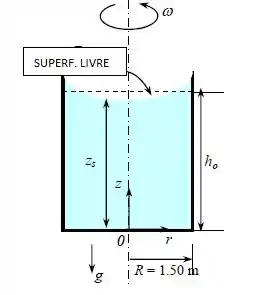
Um caminhão-tanque de leite cilíndrico vertical com 3m de diâmetro gira à taxa constante de 12 rpm. Se a pressão no centro da parte inferior da superfície for de 130 kPa, determine a pressão na borda da superfície inferior do tanque. Considere que a densidade do leite seja de 1030 kg/m³.

Passo 1

Vamos tomar o centro da superfície inferior como a nossa origem, beleza? Isso quer dizer que ali temos r = 0 e z = 0.

Para esse tipo de escoamento, a gente tem que lembrar da bendita equação que é:

z s r = h 0 - w 2 4 g R 2 - 2 r 2

Onde W é nossa velocidade angular que deve ter unidades de rad/s

Vamos substituir nossas variáveis nesse parananuê aí!!

w = 2 π n ˙ = 2 π 12 r e v m i n 1   m i n 60 s = 1,26   r a d / s

Passo 2

A altura de fluido nas bordas pode ser calculada da seguinte forma:

∆ h = z s R - z s 0 = h 0 + w 2 R 2 4 g - h 0 - w 2 R 2 4 g = w 2 R 2 2 g = 1,26   x   1,5 2 2 9,81 = 1,8   m

Passo 3

Portanto a diferença de pressão que corresponde a essa diferença de altura é nada mais e nada menos que a nossa velha equação de hidrostática:

∆ P = ρ g ∆ h = 1030 k g m 3 9,81 m s 2 1,8   m 1 k N 1000   k g . m s 2 = 1,8 k N m 2 = 1,8   k P a

Por fim, você vai concordar comigo então que a pressão nas bordas vai ser:

P b o r d a s = P c e n t r o + ∆ P = 130 + 1,8 = 131,8   k P a

Resposta

P b o r d a s = 131 ,   8   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque de água está sendo rebocado em uma estrada inclinada que faz 20° com a horizontal a uma aceleração constante de 5 m/s² na direção do movimento. Determine o ângulo que a superfície livre da á
Um aquário que contem água até 40 cm de altura é transportado na cabine de um elevador. Determine a pressão na parte inferior do tanque quando o elevador está (a) parado, (b) movendo-se para cima com
Um tanque cilíndrico de água com 60 cm de altura e 40 cm de diâmetro está sendo transportado em uma estrada plana. A maior aceleração prevista é de 4 m/s². Determina a altura inicial permitida da água
O volume de uma rocha deve ser determinado sem usar nenhum dispositivo de medição de volume. Explique como você faria isso com uma balança de mola à prova de água.