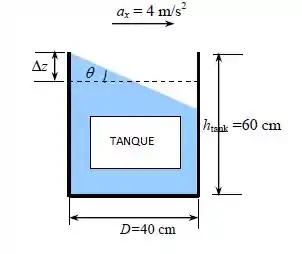
Um tanque cilíndrico de água com 60 cm de altura e 40 cm de diâmetro está sendo transportado em uma estrada plana. A maior aceleração prevista é de 4 m/s². Determina a altura inicial permitida da água no tanque se nenhuma água pode ser derramada durante a aceleração.

Na vertical, a gente observa que esse aumento da altura da água ocorre na parte de trás do tanque e NO MEIO do plano ali que a gente fez (a linha pontilhada), a gente consegue observar que a altura da água se manterá a mesma. Então a gente pode dizer que a altura máxima na parte de trás relativa ao meio do nosso plano é:

Note que a altura de água máxima inicial então no tanque a fim de evitar que haja qualquer derramamento deve ser a altura do tanque MENOS a altura máxima que a água pode subir em relação ao nosso plano, certo?