O volume de uma rocha deve ser determinado sem usar nenhum dispositivo de medição de volume. Explique como você faria isso com uma balança de mola à prova de água.

Bora lá!

A rocha tem formato irregular e a gente não conhece a densidade dela!

Primeiro a gente pesa ela em uma balança fora da água, para achar a sua força peso, :

O valor encontrado na balança vai ser a massa da rocha, , é a aceleração da gravidade!

Agora o próximo passo é pegar essa balança, coloca na água e pesar a rocha na água! Vamos olhar um esqueminha pra a gente entender melhor!

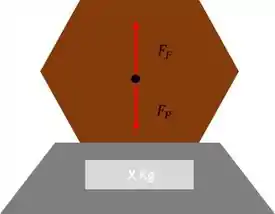
Aqui a gente tem uma figura hipotética da rocha, lembrando que a gente não conhece o seu formato! O desenho é só pra a gente entender melhor como as forças vão agir!

Existe uma força pra baixo que é a força peso e uma força pra cima que é a força de flutuação, o valor encontrado na balança quando ela esta dentro da água, nada mais é do que a massa referente a força resultante .

Mas como assim?

A a gente achou quando pesamos a rocha fora da água, agora precisamos encontrar e , vamos começar com :

Onde é a “massa da rocha quando esta dentro da água” que nada mais é do que o valor que vai aparecer na balança.

Agora para achar

A é uma função da densidade da água () da aceleração da gravidade () e do volume da rocha, , que é exatamente quem queremos encontrar!!

Agora vamos substituir as forças na equação:

Temos:

Arrumando:

Opa! Podemos cortar a gravidade!

Além disso podemos isolar :

Tcharaaaan! Conseguimos uma expressão para o volume da rocha!