Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 29
Em um campo de escoamento compressível oscilante a taxa de deformação volumétrica não é zero, mas varia com o tempo acompanhando uma partícula de fluido. Em coordenadas cartesianas expressamos isso como
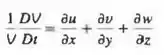
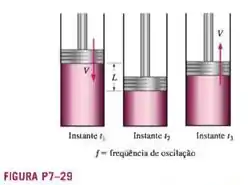
Suponhamos que a velocidade e o comprimento característicos de determinado campo de escoamento sejam V e L, respectivamente. Suponhamos também que seja uma frequência característica da oscilação (Figura P7-29). Defina as seguintes variáveis adimensionais,
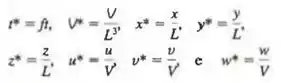
Adimensionalize a equação e identifique todos os parâmetros adimensionais usuais (nomeados) que possam aparecer.
Passo 1
Oi pessoal, tudo bem?
Bem, agora que relembramos como ocorre a adimensionalização nos problemas e utilizando as relações dadas no enunciado do problema em questão, vamos analisar a equação mostrada.
Passo 2
A equação é:
Para reescrever a Eq. 1 adimensionalizada, nós podemos substituir as variáveis não dimensionadas da equação, que já sabemos as relações, dadas no problema.
Ficou confuso?
Por exemplo, pelas variáveis definidas no enunciado, temos que, e , etc.
Assim, substituindo as variáveis não dimensionadas da equação:
Ou, simplificando:
Reconhecemos o parâmetro adimensional entre parênteses na Eq. 2 como (número Strouhal). Podemos reescrever a Eq. 2 como:
Resposta
Portanto: