Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 40

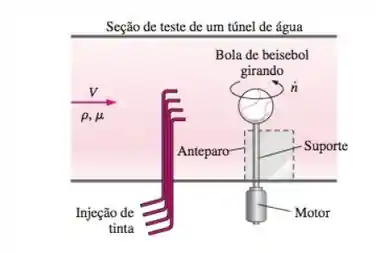
Alguns alunos querem visualizar o escomento em uma bola de beisebol girando. Seu laboratório de fluidos tem um bom túnel de água no qual eles podem injetar listras de tinta multicolorida. Assim, eles resolvem testar uma bola de beisebol girando no túnel de água. A semelhança exige que comparem o número de Reynolds e o número de Strouhal entre o modelo do teste e a bola de beisebol real que se move através do ar a 80 mi/h e gira a 300 rpm. Tanto o ar quanto a água estão a 20°C. A qual velocidade eles devem fazer a água correr no túnel de água, e a quantas rotações por minuto devem girar a bola de beisebol?

Passo 1

Nosso primeiro passo aqui vai ser pegar as propriedades da água na temperatura que está sendo dita, ou seja, 20°C.

ρ á g u a = 998   k g / m ³

μ á g u a = 1,002   x   10 - 5 k g m . s

Mas convenhamos que a gente joga beisebol na terra, né? Haha Então quando formos fazer a comparação de protótipo com modelo, vamos precisar das propriedades do ar a 20°C também.

ρ a r = 1,204   k g / m ³

μ a r = 1,825   x   10 - 5 k g m . s

Passo 2

Agora a gente vai fazer uma mágica maravilhosa que os números adimensionais nos proporcionam, que é: Os números adimensionais do modelo devem ser iguais aos do protótipo!

R e m = R e p → ρ m V m L m μ m = ρ p V p L p μ p

Lembre-se que Vp = 80 mph foi um dado no enunciado.

Vamos isolar nossa varíael de interesse, certo?

V m = V p μ m μ p ρ p ρ m L p L m = 80   x 1,002   x   10 - 5 1,825 x   10 - 5 1,204 998 1 = 5,30   m p h

Passo 3

Da mesma forma, o número de Strouhal deve ser igual!

S t m = f m L m V m = S t p = f p L p V p

Lembrando que f é proporcional ao número de rotações n ˙ e isolando nossa varíavel a ser descoberta:

n ˙ m L m V m = n ˙ p L p V p → n ˙ m = n ˙ p L p L m V m V p = 300 1 5,30 80 = 20   r p m

Resposta

V m = 5,30   m p h

n ˙ m = 20   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Problemas que envolvem dissipação viscosa de energia dependem da viscosidade μ , da condutividade témica k, da velocidade não perturbada U 0 e da temperatura não perturbada T 0 . Agrupe esses parâmetr
Reconsidere o balanço de quantidade de movimento angular da Figura 4.5 acrescentando um conjugado de corpo C z concentrado em torno do eixo z [6]. Determine a relação entre o conjugado de corpo e a te
O número de Morton, Mo, usado para correlacionar estudos de dinâmica de bolhas, é uma combinação dimensional de aceleração da gravidade g, viscosidade μ , e massa específica ρ e o coeficiente de tensã
Um corpo cai na superfície da lua (g = 1,62 m/s²) com uma velocidade inicial de 12 m/s. Usando as variáveis da opção 2, Equação (5.11), o impacto como o solo ocorre em t** = 0,34 e S**=0,84. Calcule (
Para escoamento axial através de um tubo circular, o número de Reynolds para a transição para a turbulência é aproximadamente 2300, com base no diâmetro e na velocidade média. Se d = 5 cm e o fluido é