Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 38

Isso é uma continuação do Problema 7-35. Os alunos medem o arrasto aerodinâmico em seu submarino modelo no túnel de vento. Eles tomam cuidado para fazer o túnel de vento funcionar em condições que garantam a semelhança com o submarino protótipo. Sua força de arrasto medida é 2,3 N. Estime a força de arrasto sobre o submarino protótipo nas condições dadas no Problema 7-35.

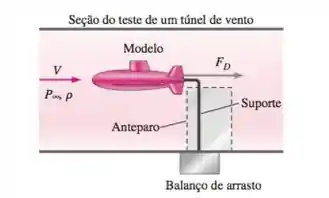
Passo 1

Uma maravilha que acontece entre os números adimensionais é que eles devem ser iguais quando se fala de protótipo e modelo.

Nesse caso precisaremos igualar os coeficientes de arrasto!!!

C D R e 2 = F D

F D R e 2 = C D

F D , m D m ρ m V m 2 L m 2 = F D , p D p ρ p V p 2 L p 2

Como Dp = Dm, temos que:

F D , m ρ m V m 2 L m 2 = F D , p ρ p V p 2 L p 2

Agora, vamos usar as propriedades da água a 15°C e Patm que podem ser obtidas em qualquer tabela de propriedades. (protótipo).

ρ = 999 k g m 3 ; μ = 1,138   x   10 - 3 k g m . s  

Também precisaremos das propriedades a 25°C (modelo).

ρ = 1184   k g m 3 ; μ = 1,849   x   10 - 5 k g m . s  

Passo 2

Vamos então isolar a força de arrasto do protótipo!!!!

Lembrando que Vp = 0,56 m/s e Vm = 61,4 m/s e a razão entre os comprimentos é de 8 pois temos uma escala tal que Lp = 8Lm (condições do exercício 7-35).

F D , p = F D , m ρ p ρ m V p V m 2 L p L m 2 = 2,3 999 1184 0,560 61,4 2 8 2 = 10,3   N

Resposta

F D , p = 10,3   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o escoamento permanente a baixa velocidade (laminar)através de um tubo circular, como representa a Figura P1.12, a velocidade u varia com o raio e assume a forma u = B Δ p μ ( r 0 2 - r 2 ) em qu
Suponha que saibamos pouco sobre a resistência dos materiais, mas nos informaram que a tensão de flexão σ em uma viga é proporcional à metade da espessura y da viga e também depende do momento de flet
Mott [49] recomenda a seguinte fórmula, no sistema inglês, para a perda de carga por atrito h P , em f t , para um escoamento através de um tubo de comprimento L e diâmetro D (ambas as medidas devem e
A convecção de Marangoni ocorre quando uma superfície tiver uma variação na tensão superficial ao longo de seu comprimento. O número adimensional de Marangoni M é uma combinação da difusividade térmic
O módulo de elasticidade volumétrica isentrópica B de um fluido é definido como a variação isentrópica da pressão pela variação fracionária da massa específica: B = ρ δ p δ ρ s Quais são as dimensões