Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 27
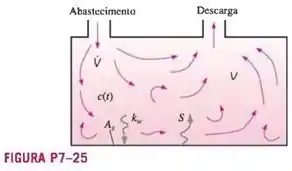
Considere a ventilação de uma sala bem misturada como aquela da Figura P7-25. A equação diferencial da concentração de massa na sala como função do tempo é dada no Problema 7-25 e é repetida aqui por conveniência,
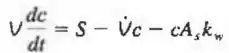
Existem três parâmetros característicos em tal situação: L, uma escala de comprimento característica da sala (considere ); V a vazão em volume do ar fresco para a sala e , a concentração máxima de massa que não é prejudicial, (a) Usando esses três parâmetros característicos, defina as formas adimensionais de todas as variáveis da equação. (Sugestão: por exemplo, defina .) (b) Reescreva a equação na forma adimensional, e identifique todos os grupos usuais adimensionais que possam aparecer.
Passo 1
Oi pessoal, tudo bem?
Primeiramente vamos assumir que:
1. O ar na sala é bem misturado, de modo que é apenas uma função do tempo.
Agora vamos relembrar um pouco como adimensionalizamos variáveis?
É o seguinte, já vimos como encontramos as dimensões das equações através das dimensões primárias (chamadas também de parâmetros de escala) de cada variável, certo?
Pois bem, a partir dessas dimensões encontradas, podemos realizar uma divisão de cada variável por uma variável arbitrária de mesma dimensão, resultando em uma variável adimensionalizada, entendido? Então mãos à obra.
Passo 2
Letra a) Vamos adimensionalizar as variáveis (uma a uma) por inspeção de acordo com suas dimensões. Então vamos lá:
Primeiro, o problema pediu para considerar , assim:
Depois, temos a sugestão de que , portanto:
O tempo é . Porém sabemos que o pode ser representado pela razão do volume pela vazão volumétrica: , pois . Então, reorganizando:
Continuando, vamos analisar a área , e como a mesma é dada em , podemos adimensionalizar como:
No Problema 7-25 encontramos que . Como já sabemos que , então , portanto temos:
E por fim:
Passo 3
Organizando as variáveis adimensionalizadas, temos:
Passo 4
Letra b) Agora nós os substituímos para gerar a equação adimensionalizada:
Notamos que todo termo na Eq. 1 contém o produto . Dividimos cada termo por essa quantidade para obter uma forma não dimensionalizada da equação:
Resposta
Portanto:
Letra a)
Letra b)