Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 17
Um canal trapezoidal com uma largura inferior de , com inclinação lateral de para , com inclinação no fundo do canal de , e um de Manning igual a , transporta uma descarga de . Calcule a profundidade e a velocidade crítica deste canal.
Passo 1
Vamos começar visualizando o canal? É um bom jeito de entender melhor o que o enunciado está nos dizendo:
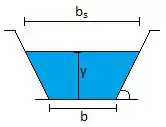
Aeee! Esse é nosso canal! Já podemos observar a largura inferior (), e aquele ângulo ali que o exercício nos disse que a inclinação lateral é de para , então conseguimos encontrar nosso ângulo:
Vamos aproveitar esse primeiro passo para fazer também as conversões:
Passo 2
Vamos agora dar uma olhada na fórmula que relaciona esses parâmetros que nós temos que calcular:
Bom, dessa forma nós ficamos com mais de uma incógnita… Masss, o enunciado nos deu a vazão...Humm...Então que tal reescrever essa equação de outra forma, de modo que apareça componentes que nós temo? Show! Então vamos lá:
Aí sim! Já melhorou um pouco!
Mas agora temos uma área de escoamento para encontrar, mas se a gente usar a tabela 11.1 através dessa equação podemos encontrá-la:
Beleza! Então vamos substituir isso na nossa equação:
Estamos no caminho certo! Partiu próximo passo!
Passo 3
A gente não pode esquecer que o exercício quer os fatores críticos, então:
Passo 4
Agora que temos uma função de com parâmetros conhecidos podemos dar valores para para que a gente ache valores para .
Já chega, né? Vamos trabalhar ! Já temos nossa profundidade! Aeeee!!
Agora partiu encontrar nossa área:
Com a área a gente já pode resolver o outro questionamento do exercício, a velocidade:
Resposta