Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 80
Usando o EES (ou outro software), calcule e represente graficamente a variação da entropia do ar através do choque normal para números de Mach a montante entre e em incrementos de . Explique por que as ondas de choque normais só podem ocorrer para números de Mach a montante maiores do que .
Passo 1
O problema é sobre choques normais no escoamento de ar. A questão pede que a gente calcule a diferença entre a entropia do ar depois do choque e antes do choque . No entanto, o problema quer que a gente calcule para diversos números de Mach do ar antes do choque . Segundo o enunciado, deve variar entre e .
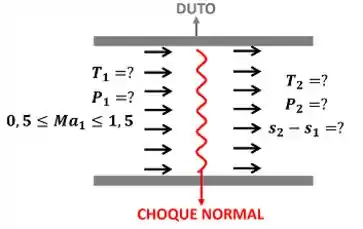
e são as temperaturas do ar antes e depois do choque normal. e são as pressões do ar antes e depois do choque normal.
Depois de calcular um para cada valor de diferente, o problema pede para a gente gerar um gráfico e uma tabela da variação de entropia versus número de Mach de entrada com esses resultados. Por fim, a questão ainda pede que a gente justifique através dos resultados o motivo de não existir onda de choque normal para .
Apesar do exercício pedir muita informação (uma tabela, um gráfico e justificativa de não existir choque normal para ), usamos uma única fórmula para calcular a variação de entropia . Como ar pode ser considerado um gás ideal com calor específico constante , podemos calcular através da fórmula de variação de entropia para um gás ideal com constante que se encontra abaixo.
é a constante de gás do ar e vale . é a pressão de saída do ar.
No próximo passo vamos aprender como usar essa fórmula!
Passo 2
Nesse passo, vamos aprender a usar a fórmula de variação de entropia para gases ideais. Para usar essa fórmula, precisamos conhecer todos os termos do lado direito da questão. No entanto, não sabemos quanto vale nem . Para calcular , usamos uma equação de choques normais que relaciona a pressão com a pressão .
onde é o número de Mach do ar antes do choque, é o número de Mach do ar depois do choque e é uma constante que vale para o ar.
Para calcular , usamos uma equação de choques normais que relaciona a temperatura com a temperatura .
Vemos que para calcular tanto quanto precisamos calcular primeiro o número de Mach do ar depois do choque . Para isso, usamos uma equação de choques normais que relaciona o número de Mach antes do choque com o número de Mach depois do choque .
Note que, a partir da equação acima, vamos encontrar valor de para cada valor de entre e . A questão pede para a gente variar de em . Ou seja, calcularemos primeiro o valor de para , depois para e assim por diante até chegar no último valor de para .
Por fim, utilizaremos cada valor de para calcular vários valores de e e substituiremos os e encontrados na fórmula de . Esses valores finais de formarão o gráfico e as tabelas!
No próximo passo aprenderemos a fazer esses cálculos repetidos de uma forma mais rápida!
Passo 3
No passo anterior nós vimos a quantidade enorme de cálculos repetidos que precisamos fazer para gerar o gráfico e a tabela de versus . Como podemos fazer isso de uma forma mais rápida?
Programando um algoritmo para fazer as contas automaticamente para a gente!
Abaixo, nós vemos um algoritmo do MATLAB feito para realizar essas contas!
No próximo passo veremos os resultados.
Passo 4
Nesse passo, será mostrado o gráfico s-Ma ( versus ) gerado pelo algoritmo do MATLAB e a tabela gerada por esse algoritmo também.
Além disso, entenderemos o motivo de não existir onda de choque normal para .
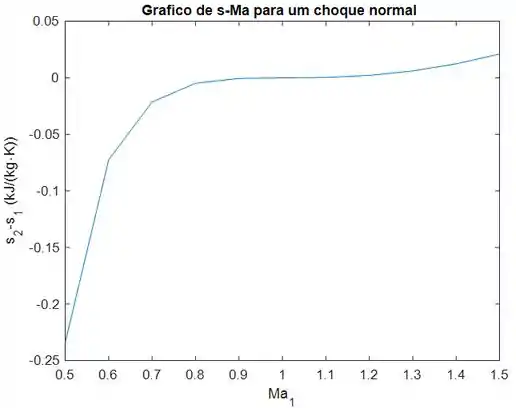
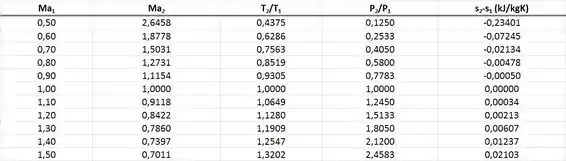
No gráfico e na tabela acima nós vemos que, para valores de número de Mach menores que 1, a variação de entropia é negativa. Isso viola a segunda lei da termodinâmica que diz que a entropia líquida só pode aumentar. Ou seja, não existe choque normal para , porque isso violaria a segunda lei da termodinâmica.
Resposta
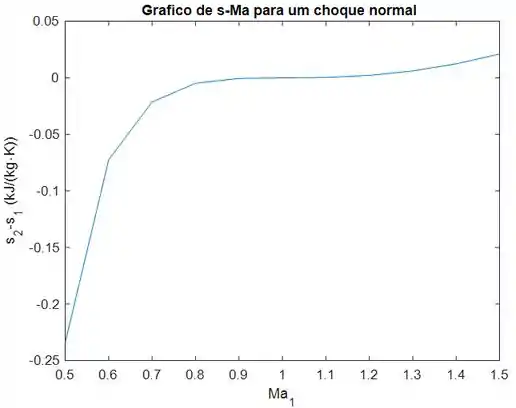
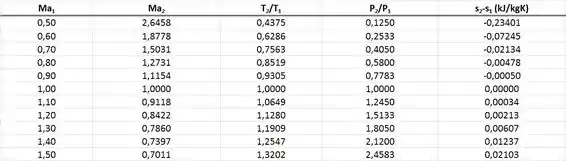
No gráfico e na tabela acima nós vemos que, para valores de número de Mach menores que 1, a variação de entropia é negativa. Isso viola a segunda lei da termodinâmica que diz que a entropia líquida só pode aumentar. Ou seja, não existe choque normal para , porque isso violaria a segunda lei da termodinâmica.