Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 18

Um canal retangular carrega uma descarga de 0,93   m 3 / s por metro de largura. Determine a energia específica mínima possível para esse escoamento. Calcule a profundidade e a velocidade de escoamento correspondente.

Passo 1

Vamos começar visualizando melhor nosso canal retangular:

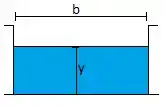
O enunciado nos dá a vazão por largura e pede há energia específica, há profundidade e há velocidade…

Relaxa! A gente tira de letra isso aí!

Vamos começar trocando há unidade:

Q b = 0,93   m 3 s . m → Q b = 10   f t 3 s . f t

Passo 2

A nossa fórmula de energia diz o seguinte:

E = y + V 2 2 * g

E sabemos que:

V = Q A

Nossa área é a do retângulo, beleza?

V = Q b * y

Agora colocando essa velocidade na nossa fórmula:

E = y + Q b * y 2 2 * g

E = y + Q 2 b 2 * y 2 2 * g

E = y + Q 2 2 * g * b 2 * y 2

Passo 3

Para encontrar nossos parâmetro críticos:

d E d y = 0

1 - Q 2 g * b 2 * y 3 = 0

Opa! Já dá pra achar nossa profundidade:

1 - Q 2 b 2 * 1 g * 1 y 3 = 0

y = Q 2 b 2 * g 1 3

y = 1,46   f t

Aeee! Agora só falta há velocidade e a energia…

Passo 4

Com a profundidade é só há gente voltar na fórmula lá de cima e achar a velocidade:

V = 10 1,46

V = 6,85   f t / s

Beleza! Agora a gente volta na primeira fórmula e encontrar a energia:

E = 1,46 + 6,85 2 2 * g

E = 2,19   f t

Arrasamos muitoo!

Resposta

y = 1,46   f t V = 6,85   f t / s E = 2,19   f t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12-69C Considere o escoamento de ar supersônico que se aproxima do nariz de uma cunha bidimensional e experimenta um choque oblíquo. Sob quais condições um choque oblíquo sedestaca do nariz da cunha e
Um gás ideal com k = 1,4 escoa através de um bocal de forma que o número de Mach seja 2,4 e a área de escoamento, 25c m 2 . Considerando o escoamento isentrópico, determine aárea de escoamento no loca
Repita o Problema 12-58 para um gás ideal com k=1,33 .
12-60 Ar a 900k P a e 400K entra em um bocal convergente com velocidade desprezível. A área de garganta do bocal é de 10 c m 2 . Considerando o escoamento isentrópico, calcule e faça um gráfico da pre
Ar que escoa a 60k P a , 240K e ao número de Mach 3,4 é imposto a uma cunha bidimensional de semi-ângulo 12 ° . Determine os dois ângulos de choque oblíquo possíveis, β f r a c o e β f o r t e , que p