Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 88
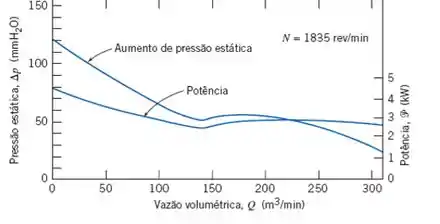
As características de desempenho de um ventilador de fluxo axial de Howden Buffalo são apresentadas na figura. O ventilador é utilizado para operar um túnel de vento de de seção transversal. O túnel consiste em uma contração de entrada suave, duas telas (casa uma com coeficiente de perda ), a seção de teste e um difusor, onde a seção transversal é ampliada para o diâmetro de na entrada do ventilador. O fluxo de ventilador é descarregado de volta no ambiente. Calcule e trace a curva característica de perda de pressão do sistema vazão volumétrica. Estime a máxima velocidade do escoamento de ar disponível na seção de teste desse túnel de vento.
Passo 1
Equação de Bernoulli:
Considerações:
;
;
;
Perdas nas telas e difusor.
Aplicando as considerações:
Sendo:
Temos:
Passo 2
Temos que é dado:
Com
Então:
Desse modo:
Passo 3
O sistema operará onde as curvas se cruzam.
No gráfico dado, isso ocorre em .
Então:
Passo 4
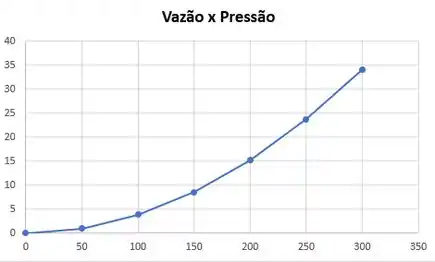
Traçando a curva característica de perda de pressão do sistema vazão volumétrica.
