Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 110
Equações para o empuxo, potência e eficiência de dispositivos de propulsão foram deduzidas na seção 10.6. Mostre que aquelas equações podem ser combinadas para a condição de empuxo constante para obter:
Passo 1
Tá legal! Vamos começar o exercício ilustrando o problema, conforme vimos nessa seção do livro, então, temos:
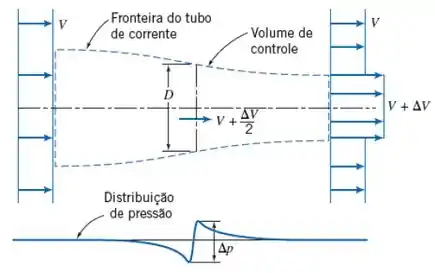
Então, a partir da equação do equilíbrio de momento na direção apresentado no capítulo 4, temos:
Então, para o sistema de controle desenhado, onde podemos desprezar as forças de campo na direção , ou seja, , e temos regime permanente, então podemos zerar a derivada parcial no tempo, temos:
No entanto, devido a continuidade do sistema, sabemos que a vazão mássica é constante, então, temos:
Então, substituindo isso na equação anterior, e sabendo que e temos:
Passo 2
Agora vamos aplicar a equação de equilíbrio de energia, também vista no capítulo 4, onde temos:
Como não temos calor entrando ou saindo do sistema, temos , não temos força de cisalhamento ou trabalhos sobre o sistema que não a potência do jato, então . Como o regime de escoamento é permanente, podemos desprezar também a integral com a derivada parcial no tempo e a equação se resume a:
A única propriedade do escoamento que varia nesse caso é a velocidade entre os pontos 1 e 4, então podemos cancelar todos os outros pontos. Vimos no passo 1 a continuidade do sistema, que nos dava:
E, também sabemos, do esquema do passo 1, que e que , então, a equação anterior se torna:
Esse trabalho é o trabalho ideal do sistema, sem considerar perdas.
Passo 3
Agora vamos aplicar a equação da continuidade para o sistema, apresentada no passo 1, onde temos:
Então, temos:
Tá legal, sabemos que a eficiência é dada por:
Já encontramos a expressão para , agora, para encontrar o trabalho útil, basta multiplicar a força encontrada no passo 1 pela velocidade de entrada do fluido no sistema , então, temos:
Substituindo as expressões encontradas na equação para a eficiência, temos:
Agora simplificando a expressão colocando o termo em evidência no denominador, temos:
Vamos deixar essa equação de lado por enquanto.
Passo 4
Agora vamos retornar à equação para encontrada no passo 1:
E vamos substituir a expressão encontrada para a vazão mássica no passo 3:
Então, manipulando a expressão para deixarmos em função do termo encontrado na equação da eficiência do passo 3, para isso precisamos colocar em evidência, então:
Agora, para encontrar um valor para , vamos chamar essa relação de , então a equação se torna:
Passo 5
Então, resolvendo essa equação do 2° grau através de Bháskara, temos:
Então, pegando a raiz positiva do resultado, temos:
E, substituindo esse valor na expressão encontrada no passo 3 para a eficiência, temos:
Multiplicando a equação em cima e em baixo por 2, temos:
Somando os termos e do denominador e jogando o de dentro da raiz para a parte de baixo para ficarmos com a equação igual a do enunciado, temos:
Resposta
Ei, a resposta está no passo a passo :)