Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 103
Uma pequena turbina hidráulica de impulsão é alimentada com água através de um tubo adutor, com diâmetro e comprimento ; o diâmetro do jato é . A diferença de elevação entre a superfície da água no reservatório e a linha de centro do bocal é . O coeficiente de perda de carga no bocal é e o coeficiente de perda de carga do reservatório para a entrada do adutor é . Determine a velocidade do jato de água, a vazão volumétrica e a potência hidráulica do jato, para o caso em que , , , , e , se o tubo é de aço comercial. Faça um gráfico da potência do jato como uma função do seu diâmetro para determinar o diâmetro ótimo e a potência hidráulica resultante do jato. Comente sobre os efeitos de variação dos coeficientes de perda e da rugosidade do tubo.
Passo 1
Equação de Bernoulli:
Considerações:
;
;
Perdas menores desprezíveis.
Com as considerações, temos:
Passo 2
Pela continuidade:
Então:
Isolando :
para tubo de aço comercial é .
Então , numa faixa considerável, pela Fig. 8.13, adotaremos .
Substituindo os dados na equação:
Assim, a vazão se dá:
E a potência hidráulica:
Passo 3
Traçando um gráfico da potência do jato como uma função do seu diâmetro para determinar o diâmetro ótimo e a potência hidráulica resultante do jato.
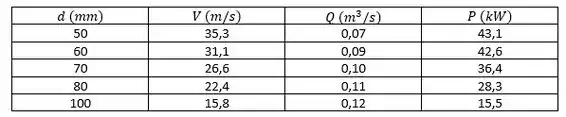
A potência máxima é atingida com .
Passo 4
Coeficientes de perda de carga têm um efeito menor, fazendo com que e aumentem o
Já a rugosidade do tubo tem um efeito maior, também aumentando gradativamente .