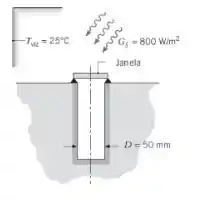
Uma cavidade profunda, com 50 mm de diâmetro, apresenta um comportamento que se aproxima do comportamento de um corpo negro. Ela é mantida a 250°C quando exposta à irradiação solar com 800 W/m2 , com a vizinhança e o ar ambiente a 25°C. Uma janela fina com transmissividade e refletividade espectrais de 0,9 e 0,0, respectivamente, na faixa espectral compreendida entre 0,2 e 4 μm, é colocada sobre a abertura da cavidade. Na região espectral além dos 4 μm, a janela se comporta como um corpo cinza, opaco e difuso, com emissividade de 0,95. Supondo que o coeficiente de transferência de calor por convecção sobre a superfície superior da janela seja de 10 W/(m2 · K), determine a temperatura da janela e a potência necessária para manter a cavidade a uma temperatura de 250°C.

Fazendo balanço de energia temos:

Tá faltando algumas coisinhas aí, né? Partiu então!

Vamos achar o e , calculando :e depois visitando a tabela 12.2, teremos:

E agora sim vamos ficar com:

Agora vamos para o próximo, do mesmo jeitinho, mas agora com a temperatura diferente:

Vamos achar novamente o e , calculando e visitando a tabela 12.2:

Vamos ficar com:

E usando o mesmo esquema novamente para achar :

Vamos achar mais uma vez o e , calculando e visitando a tabela 12.2:

Vamos ficar com:

Sendo nossa emissividade:

Vamos ter nossa temperatura como:

ou

Show de bola! Mas ainda falta achar a potência…

Agora tendo um , para achar a potência vamos fazer um novo balanço de energia:

Precisamos achar e , vamos nessa:

A potência será então:

Prontinhos! Arrasamos!