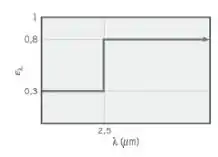
Um corpo de prova, com 10 mm de espessura e inicialmente a 25°C, deve ser temperado a uma temperatura acima de 725°C por um período de pelo menos 5 min e depois resfriado. O corpo é opaco e difuso, e a distribuição espectral de sua emissividade é mostrada na figura. O aquecimento é efetuado em uma grande fornalha com paredes e ar circulante a 750°C e um coeficiente convectivo de 100 W/(m2 · K). As propriedades termofísicas do corpo de prova são ρ = 2700 kg/m3 , c = 885 J/(kg · K) e k = 165 W/(m · K).

1. Calcule a emissividade e a absortividade do corpo de prova quando ele é colocado na fornalha com sua temperatura inicial de 25°C.
2. Determine o fluxo térmico líquido para a peça nesta condição inicial. Qual é a correspondente taxa de variação da temperatura do corpo, dT/dt?
3. Calcule o tempo necessário para o corpo ser resfriado de 750°C até a temperatura segura para o toque de 40°C, com a temperatura da vizinhança e a temperatura do ar de resfriamento iguais a 25°C, e um coeficiente convectivo igual a 100 W/(m2 · K).

Começando pela letra a, nosso enunciado pede a emissividade e a absortividade do corpo de prova…

Vamos primeiro pela emissividade:

Vamos achar esse cara , para isso vamos fazer:

Visitando a tabela 12.2, vamos ter:

E nossa emissividade ficará:

Falta ainda achar , usando a equação 12.52, vamos lá!

Vamos achar esse novamente, porque agora nossa temperatura é diferente, vamos fazer da mesma maneira:

Visitando a tabela 12.2:

Opa! Agora podemos voltar lá:

Show de bola! Partiu letra b!

Na letra b, precisamos encontrar o fluxo térmico líquido e a variação de temperatura, vamos começar usando balanço de energia:

ou

Ainda na letra b, precisamos encontrar a variação da temperatura… Vamos lá!

Uhul! Conseguimos!