Após serem cortadas de um grande lingote monocristalino e polidas, pastilhas de silício passam por um processo de têmpera a alta temperatura. Uma técnica para o aquecimento das pastilhas é a irradiação de sua superfície superior usando lâmpadas halógenas de alta intensidade com uma distribuição espectral que se aproxima à de um corpo negro a 2800 K. Para determinar a potência da lâmpada e a taxa na qual a radiação é absorvida pela pastilha, o projetista do equipamento necessita conhecer sua absortividade como uma função da temperatura. O silício é um material semicondutor que exibe um limite de banda característico e sua absortividade espectral pode ser idealizada como mostrado na figura. Em baixas e moderadas temperaturas, o silício é semitransparente em comprimentos de onda maiores do que o do limite de banda, mas se torna quase opaco acima de 600°C.
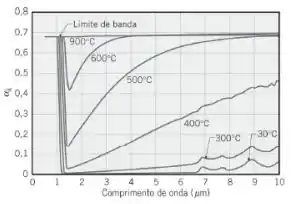
- Quais são os limites de 1% da banda espectral que incluem 98% da radiação de corpo negro correspondente à distribuição espectral das lâmpadas? Em qual região espectral você precisa conhecer a absortividade espectral?
- Como você espera que a absortividade total do silício varie como uma função de sua temperatura? Esboce a variação e explique suas principais características.
- Calcule a absortividade total da pastilha de silício para a irradiação das lâmpadas e cada uma das cinco temperaturas mostradas na figura. Destes dados, calcule a emissividade da pastilha a 600 e 900°C. Explique os seus resultados e o porquê da emissividade variar com a temperatura. Sugestão: No IHT, disponível no site da LTC Editora, crie uma tabela para especificar valores das propriedades espectrais e as funções LOOKUPVAL e INTEGRAL para efetuarem as integrações necessárias.
- Se a pastilha estiver no vácuo e a troca radiante somente ocorrer em uma face, qual é a irradiação necessária para manter a temperatura da pastilha em 600°C.
Passo 1
Fala aí! Partiu fazer essa questãozinha!
Vamos começar pela letra a, nosso enunciado pede pra gente os limites de 1% da banda espectral que incluem 98% da radiação de corpo negro…
Visitando a tabela 12.2, nós temos que:
Para vamos ter
e
Para temos
Para a gente conhecer as várias regiões espectrais, dentro dos limites, vamos fazer o seguinte, sendo:
e
e
Teremos, com :
e
e
Com :
e
e
Com :
e
e
Com :
e
e
Precisamos conhecer a região, para a irradiação no corpo negro, onde … A região espectral será entre e .
Passo 2
Na letra b, a gente precisa esboçar como a absortividade varia… Segundo a equação 12.52, teremos:
De acordo com os resultados da letra a, vamos esboçar o gráfico da absortividade por temperatura, como sendo:
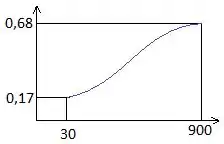
Show! Pra fechar vamos resolver a letra d!
Passo 3
Na letra d, precisamos encontrar irradiação, , vamos começar usando balanço de energia:
Assumindo:
e
e sendo , teremos o seguinte:
ou
Uhul! Conseguimos!
Resposta
- Passo 1.
- Passo 2.
- Precisa do uso de software.