Células a combustível individuais, como a do Exemplo 1.5, podem ser escalonadas através de sua organização em uma pilha de células a combustível. Uma pilha é constituída por múltiplas membranas eletrolíticas que são colocadas entre duas placas bipolares eletricamente condutoras. Ar e hidrogênio são alimentados em cada membrana através de canais de escoamento no interior de cada placa bipolar, como mostrado no esquema.

Com esta montagem da pilha, as células a combustível individuais estão conectadas eletricamente em série, produzindo uma voltagem na pilha de Epilha = N × Ec, em que Ec é a voltagem produzida através de cada membrana e N é o número de membranas na pilha. A corrente elétrica é a mesma em cada membrana. A voltagem da célula, Ec, assim como a eficiência da célula, aumenta com a temperatura (o ar e o hidrogênio alimentados na pilha são umidificados para permitir a operação em temperaturas superiores a do Exemplo 1.5), porém as membranas irão falhar em temperaturas excedendo T ≈ 85°C. Considere membranas com L × w, em que L = w = 100 mm, e espessura tm = 0,43 mm, as quais cada uma produz Ec = 0,6 V a I = 60 A, e Ėc,g = 45 W de energia térmica quando operando a T = 80°C. As superfícies externas da pilha estão expostas ao ar a = 25°C e à vizinhança a Tviz = 30°C, com ε = 0,88 e h = 150 W/(m2 · K).

(a) Encontre a potência elétrica produzida por uma pilha com comprimento Lpilha = 200 mm, para espessuras das placas bipolares na faixa de 1 mm

(b) Calcule a temperatura superficial e explique se a pilha necessita ser internamente aquecida ou resfriada para operar na temperatura interna ótima de 80°C para várias espessuras da placa bipolar.

(c) Identifique como a temperatura interna de operação da pilha pode ser diminuída ou elevada para uma dada espessura da placa bipolar e discuta mudanças no projeto que promoveriam uma distribuição de temperaturas no interior da pilha mais uniforme. Como variações nas temperaturas do ar externo e da vizinhança afetariam a sua resposta? Qual membrana na pilha é mais passível de falha em função de uma alta temperatura de operação?

Para resolver o item (a), vamos analisar o esquema da pilha na figura abaixo:

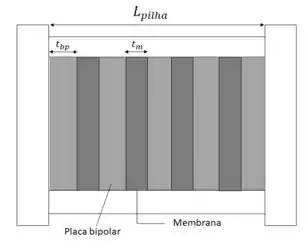
Como é possível observar, para cada mebranas, temos placas bipolares. Portanto, podemos expressar a espessura da pilha, , relacionando com a espessura de cada membrana, , e a espessura de cada placa bipolar, :

Podemos reorganizar para explicitar o valor de :

Segundo o enunciado devemos considerar uma espessura de cada placa em duas situações: 1 e 10 .

Para :

Para :

Sendo a potência elétrica , vamos calcular a potência elétrica produzida pelas pilhas com e , respectivamente:

Sendo a energia térmica , vamos calcular as energias térmicas liberadas pelas pilhas com e , respectivamente:

Vamos resolver agora o item (b).

O balanço de energia para a superfície externa da pilha basicamente pode ser descrito de forma a igualar toda a energia térmica gerada (calculada na última etapa do Passo 2) a dissipação por convecção e radiação:

Agora vou mostrar as equações que vamos utilizar para calcular as taxas convectiva e radiante:

A área é uma soma das áreas dos seis lados da pilha:

Agora, vamos deixar então a nossa taxa convectiva em função da temperatura da superfície :

0

Já para calcular a taxa de emissão por radiação, devemos substituir a emissividade dada pelo problema, a constante de Stefan-Boltzmann (σ = ), área e as temperaturas da superfície e da vizinhança. Lembre que para calcular taxas radiantes, devemos colocar as temperaturas em Kelvin!

Sendo assim:

Agora, iremos calcular as temperaturas da superfície para duas situações: pilhas com e . O que muda em cada situação é a energia térmica produzida que calculamos no passo anterior.

Para , o balanço de energia se torna:

Reorganizando a equação para explicitar :

Para encontrar o valor de basta resolver a equação acima. Nesta resolução, foi utilizado o método de busca direta em uma calculadora, mas você pode se sentir livre para resolver da maneira que desejar. Sendo assim:

Ou seja, para placas bipolares de espessura , a pilha deve ser internamente resfriada para atingir a temperatura superficial de .

Para , o balanço de energia se torna:

Reorganizando a equação para explicitar :

Para encontrar o valor de basta resolver a equação acima. Nesta resolução, foi utilizado o método de busca direta em uma calculadora, mas você pode se sentir livre para resolver da maneira que desejar. Sendo assim:

Ou seja, para placas bipolares de espessura , a pilha deve ser internamente aquecida para atingir a temperatura superficial de .

Vamos responder agora a letra (c).

Para diminuir a temperatura interna da pilha, poderia ser utilizada convecção forçada com auxílio de um ventilador, por exemplo. Além disso, poderíamos aumentar as dimensões das placas bipolares para aumentar a taxa de transferência de calor.

Para manter a temperatura das pilhas uniforme, poderiam ser utilizados materiais de maior condutividade térmica, que não teriam grande resistência à transferência de calor.

Além disso, se aumentarmos a temperatura externa, também aumentaremos a temperatura da superfície. Se diminuíssemos a temperatura externa, também diminuiríamos a temperatura superficial.

Por fim, a membrana que apresentaria a maior probabilidade de falha é aquela mais distante do resfriamento, no meio da pilha.